A R Guide by Samuele Carcagno sam.carcagno@gmail.com is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Based on a work at https://github.com/sam81/rguide.

The latest html version of this guide is available at https://sam81.github.io/r_guide_bookdown/rguide.html

A pdf version of this guide can be downloaded at https://sam81.github.io/r_guide_bookdown/rguide.pdf

Associated datasets available at https://sam81.github.io/r_guide_bookdown/rguide_datasets.zip

Associated code available at https://sam81.github.io/r_guide_bookdown/rguide_code.zip

Preface

I started writing this guide in 2006 while I was learning R. It was always a work in progress, with incomplete bits and parts, and it wasn’t updated for several years. Much has changed since then both in the R ecosystem, and in the way I use R for data analysis. I’m now in the process of revising it to reflect these changes. Because this guide was initially written when I still had very little knowledge not only of R but of programming in general, it tends to explain things with a very simple, beginner-friendly approach. I hope to maintain this aspect of the guide as I revise it. This remains very much a work in progress and comes with NO WARRANTY whatsoever of being correct in any of its parts.

For me, this is like a R desk reference. Once I figure out some new useful function, how to solve a particular problem in R, or how to generate a certain graphic, I write it down in this guide. Next time I have to solve the same problem I quickly know where to find the answer, rather than wading through internet forums, stack overflow, or other websites hunting down for the answer.

1 Getting started with R

1.1 Installing R

The information on installing R provided in this section is relatively generic and limited. For detailed information please refer to the “R Installation and Administration Manual” available at the CRAN website https://cran.r-project.org. CRAN stands for “Comprehensive R Archive Network”, and is the main point of reference for the R software. There you can find R sources, binaries, documentation, and add-on packages.

1.1.1 Installing the base program

First of all you need to install the base R program. There are two ways of doing this, you can either compile the source code yourself, or you can install the precompiled binaries for your specific operating system. The second way is the easiest one, and usually you will want to go with it.

1.1.1.1 GNU/Linux and other Unix systems

Precompiled binaries are available for some GNU/Linux distributions, there is a list of these on the R FAQ. For other distributions you can build R from source. There are precompiled binaries for Debian GNU/Linux, so you can install the R base system and a number of add-on packages with the usual methods under Debian, that is, by using apt-get, or a graphical package manager such as Synaptic, or whatever else you normally use.

1.1.1.2 Windows

There are precompiled binaries for Windows, you just have to download them, then double click on the installer’s icon to start the installation. Most Windows versions are supported.

1.1.1.3 Mac Os X

Precompiled binaries are also available for Mac Os X, you can download them and then double click on the installer’s icon to start the installation.

1.1.2 Installing add-on packages

There is a vast number of add-on packages (for a categorized view see CRAN task views) that implement statistical functions that are not available with the base program. They’re not strictly necessary, but if you keep using R, sooner or later you will want to install some of these packages.

1.1.2.1 GNU/Linux and other Unix systems

There are different ways to get packages installed. For Debian there are precompiled versions of some packages, so you can get them with apt-get or whatever else you usually use to install Debian packages; this will also take care of possible dependencies (some packages need other packages or system libraries to be installed in order to work). For other packages, from an R session you can call the install.packages function, for example:

install.packages("gplots")

will install the gplots package. You can also install more than one package in one go:

install.packages(c("gplots", "signal"))

will install the gplots and signal packages. Another way to install a package is to download the related tarball from CRAN and then from a console issue the command:

R CMD INSTALL /packagename

where packagename is the full path to the tarball you have downloaded. There are other ways and other specific options to install add-on packages. You should refer to the “R Installation and Administration Manual” for further information.

1.1.2.2 Windows

The R graphical user interface (GUI) on Windows provides an interface to download and install the packages directly from the internet.

1.2 A simple introduction to R

This section will give a simple introduction to R, just to get familiar with it and get a general idea of how it works. This section assumes no previous knowledge of programming. If you know other computer languages, or have even a basic knowledge of programming, getting started will be easy. If you don’t, don’t worry, R syntax is very elegant and simple, it might take a little while, but after looking at some examples, and importantly, trying them out yourself, you’ll be up and running without problems. This tutorial deals only with learning to use R from the command line, if you’d rather use R with a GUI, that is, with a “point and click” interface, please have a look at Section 1.2.6 for some information on how to get started.

1.2.1 Datasets

This guide uses several datasets. If you want to follow the examples given in the guide you can download the datasets from this URL: https://sam81.github.io/r_guide_bookdown/rguide_datasets.zip

1.2.2 Firing up and quitting R

Under GNU/Linux systems you can start R from a shell, just type R and press Enter. Under Windows you can click on the R icon to start the R GUI.

You can save yourself a lot of typing by using the up arrow key ↑ to retrieve past commands.

Commands can be terminated either by a semi-colon ; or by pressing Enter and starting a newline. If you start a newline before a command is complete, R will prompt you to complete the command with a + sign, you can then complete the command. If you don’t know how to complete the command and get stuck, you can stop R prompting you with the plus sign by pressing the CTRL and C keys simultaneously.

To quit R type quit() or q(), R will ask you if you want to save the current session, if you answer y, R will save all the objects active in the current session and the command history.

1.2.3 Starting to work with R

The first thing you can try, is doing some math, at the command prompt type 5+4 and press Enter, the result will be

5 + 4

## [1] 9

well, obviously 9. Other arithmetic operators are listed in Table 1.1

Table 1.1: Arithmetic Operators.
Symbol	Function
`+`	Addition
`-`	Subtraction
`*`	Multiplication
`/`	Division
`^`	Exponentiation

Now let’s create a variable, we’ll call it foo, and assign to it a number

foo = 5

the equal sign = is the assignment operator in R, in the above case it means “the value of foo is 5”, foo is an object. The “arrow symbol”, constructed by a “less than” sign followed by a dash, <-, can also be used as an assignment operator, and foo = 5 is equivalent to

foo <- 5

In R both = and <- can be used as assignment operators. For example, the expression x = 5 and the expression x <- 5 are equivalent, and both are in common use, although some style guides recommend one over the other. In a few corner cases using <- instead of = may lead to different behaviors (e.g. when trying to make assignments inside function calls; something that you generally shouldn’t do).

I tend to stick to using = because it requires only a single keystroke, looks more readable to me, and is the assignment operator used in almost all other programming languages.

Because foo is an object of numeric type, we can perform arithmetic operations on it:

foo * 2

## [1] 10

we can also store the results of an arithmetic operation in an object:

another_foo = 5^2

if you want to display the value of this new object you can use

print(another_foo)

## [1] 25

or, for short, just type its name and press Enter

another_foo

## [1] 25

since the two objects we have created are both numeric we can also sum them:

foo + another_foo

## [1] 30

In R variable names can be made up of letters, numbers, and the underscore (_), or the dot (.) characters. For example foo, foo1, foo_1, and foo.1 are all syntactically valid variable names. However, there are some restrictions; for example variable names cannot start with a number, or with an underscore. Also, there are reserved keywords, such as for, if, else, that cannot be used as variable names. For more info see the help page for make.names by typing ?make.names in the R interpreter.

Let’s look at something more interesting, we can create an object that stores a series of numbers, for example the money we have spent each day of a week, in Euros; we can do this using the c function, which concatenates a series of values into a vector:

expenses = c(7, 8, 15, 20, 9, 45, 3)

you might want to find out how much you’ve spent on average during the week, this is easily accomplished with the function mean

mean(expenses)

## [1] 15.28571

the function sd gives you the standard deviation

sd(expenses)

## [1] 14.24446

Surely you’ve wondered why [1] appears every time R gives you a result, now that we’ve introduced the vector we can get to it. Try to create a long vector, you can easily do this by creating a sequence of numbers, for example:

long_vec = seq(1, 100, by=1)

will create a vector containing the sequence of numbers from 1 to 100, now try to display it and see what happens. All the elements of the vector won’t fit in a single line of the screen, and at the start of each line you’ll get between the index, that is the position, of the first element on that line. There’s also a shorthand to create such a vector:

long_vec = 1:100

R can also deal with string variables:

name = "John"
msg1 = "said to check the supplies"

strings can be concatenated together with the paste function:

paste(name, msg1)

## [1] "John said to check the supplies"

by default strings pasted together with the paste function are separated by a blank space, but this can be changed by supplying a sep argument to the function:

paste(name, msg1, sep=";")

## [1] "John;said to check the supplies"

if we want the strings to be attached together with no separator at all, we can write paste(name, msg1, sep=""), but it is more convenient to use the paste0 function instead:

paste0(name, msg1)

## [1] "Johnsaid to check the supplies"

more string facilities are presented in Section 4.3.

1.2.4 Using R packages

As mention in Section 1.1.2 there are many add-on packages, with additional statistical and graphical functions for R. That section had some instructions on how to install them, but did not explain how to use them. In order to use a function from a package that you have already installed you can load the package with the library function. For example, if you want to use the geometric.mean function from the psych package in order to compute the geometric mean of a set of numbers you can run the following commands:

library(psych)
geometric.mean(c(4, 54, 7, 15))

## [1] 12.27187

Loading a package in this way will import all the functions of that package in the current namespace, in other words, this lets you call directly those functions from the current session. Occasionally there may be “clashes” in the namespace; suppose there is another package called foz (I’m making it up) tha you also need to use in your session. Package foz also happens to have a function called geometric.mean that behaves slightly differently from the function in the psych package. If you load package foz after package psych, the geometric.mean function from foz will mask the one from psych (you will get a warning on the R terminal). So, what can you do if you want to use the geometric.mean function from psych when it’s masked? You can call it with the following syntax:

psych::geometric.mean(c(4, 54, 7, 15))

## [1] 12.27187

note that this syntax works also if the psych package is not loaded, in other words you can call functions from packages with the pkgname::fncname syntax without loading the package.

1.2.5 Getting help

R comes with an excellent online help facility which documents and gives examples for all available functions. There is also a web interface for the help system which is easier to use, you can start it with

help.start()

this fires up a web browser from which you can access a search engine for all the available documentation. The documentation is also available as a pdf file, the `Full Reference Manual'' which documents the base system. Printablepdf` manuals are also available for all the other additional packages.

1.2.5.1 The online help system

You can quickly look up the documentation for a function, for example sd, with

?sd

help(sd)

it is often indifferent using quotes or not, but sometimes they are required, for example

?* ## doesn't work
Error: syntax error
?"*"  ## this works!

to quit the help screen press Q.

You can easily run the example code given in the help pages for a given function with

example(function_name)

it is better to set the graphics parameter ask as TRUE before running the examples

par(ask=TRUE)

to pause between successive plots, if there is more than one.

The online help system searches by default the available documentation for the base system and all the packages that are currently loaded. If you want to look the documentation for a function present in a package that is not loaded, you need to specify the package in question:

help("levene.test", package=car)

if you know the function exists but don’t know the package it is in, try

help(levene.test, try.all.packages=TRUE)
Help for topic 'levene.test' is not in any loaded package but can be
found in the following packages:

Package               Library
car                   /usr/lib/R/site-library

The function help.search can be used when you don’t exactly know the name of the function you’re looking for

help.search("levene")
Help files with alias or concept or title matching 'levene' using
fuzzy matching:


levene.test(car)        Levene's Test
...

1.2.6 Working with a graphical user interface

The default version of R for Windows and macOS comes with a very limited graphical user interface (GUI), while the GNU/Linux version comes with no GUI at all. There are, however, several independent projects aimed at developing a GUI for R. The following sections give info on some of them.

1.2.6.1 R Studio

R Studio is currently the most popular GUI for R. It can be installed on all major operating systems: https://www.rstudio.com.

1.2.6.2 The R Commander

An extensive GUI for R is provided by the Rcmdr package (R commander). This GUI allows you to do many of the operations you can do using R from the command line, through a point and click visual interface. The R commander is just a R package, so in order to use it, you need to have R installed in the first place, then you have to install the Rcmdr package and all the other packages it depends on. After everything is installed correctly, fire up R and call the R commander as you do with any other package:

library(Rcmdr)

you will be greeted by a GUI with menus that allow you to type in data, perform statistical analyses and create graphs. The R commander works on both GNU/Linux and Windows platforms. For further information, please refer to the R commander manual or look up the following web page: http://www.rcommander.com/.

1.2.6.3 JGR

The JGR package provides a clean, simple graphical user interface for R, which is platform independent. The package is written in JAVA and requires the JAVA SDK to run. More info is available at the project webpage: https://www.rforge.net/JGR/

2 Organizing a working session

2.1 Setting and changing the working directory

The command getwd displays the pathname of the current working directory, that is where R will look for and store files if not otherwise instructed.

To change the current working directory, use the command setwd("dirname"), where dirname is the pathname of the working directory you’re moving into. Note that this has to be an existent working directory, because R cannot create a new directory with this command. Here’s an example of how to specify the pathname on Windows:

setwd("C:/mydata/rats")

note that you have to use a slash "/" and not backslash "\" like you usually do in Windows to specify the pathname. On Unix-based OSs the pathname is specified as it would be in a shell command, e.g.:

setwd("/home/user123/Documents/analysis_exp_xyz")

You can also specify a pathname relative to your current working directory, without specifying the full pathname. It is indifferent using single ' ' or double " " quotes, this holds true when you need to quote character strings. For example to change the working directory up one level in the directory hierarchy you can write:

setwd("../")

If you want to see the files present in your current working directory you can use:

dir()

It is also possible to issue commands to the OS from within R with the system function, for example

system("ls")

under GNU/Linux or Unix systems, will list the files present in the current directory.

2.2 Objects

All the variables, functions, arrays etc…, that you work with in R are stored and manipulated as objects. To list all the objects currently active in your workspace, you can use the command:

objects()

or alternatively

ls()

if you want to remove some of these objects from memory, you can use the command:

rm(X, Y, W, foo, rats)

you can also give the variables to be removed, as a character vector:

rm(list=c("X", "Y", "foo", "rats"))

if you want to remove all the objects in your workspace, you can combine the ls and rm commands as follows:

rm(list=ls())

this however doesn’t remove objects whose name starts with a dot, to remove also those you can use:

rm(list=ls(all=TRUE))

2.3 Saving and using the “workspace image”

You can use a ``workspace image’’ that you have previously saved by starting R from the directory in which it was saved. In this way you can use the objects created in a previous session and the up arrow as well to retrieve commands from that session. To take full advantage from workspace images you’d better use different working directories for different analyses, studies, experiments and so on, in this way you can restore the workspace image of a specific analysis you were running and above all, you avoid accidentally overwriting objects from different analyses by creating another object with the same name during your current analysis.

When saving the workspace image R stores two files in the current working directory, one with the objects and one with the command history. This files begin with a dot under GNU/Linux and so are hidden.

You can save the workspace image either on exit, answering yes to the prompt you’re given, or during a session with the save.image function, the latter is a good measure against accidental losses of objects due to a power failure.

2.4 Working in batch mode

2.4.1 Executing commands written in a file from an R session

Instead of writing and executing commands line by line, it is often convenient to write the commands in a text file and then run them all at once in batch mode. You just write the commands with a text editor in a file, as if it were on the R console, save it in a directory, and then from within an R session issue the command:

source("C:mydata/myfile.txt")

By default R displays only the results of the commands written in the source file, you can change this using the option:

source("C:mydata/myfile.txt", echo=TRUE)

2.4.2 Executing commands written in a file from a shell

It is also possible to execute R commands written in a file without starting an R session: From within your system’s shell (for example bash on GNU/Linux or dos on Windows) issue the command

  $ R CMD BATCH myfile.R

where myfile.R is the file you’ve written the R commands in.

3 Data types and data manipulation

3.1 Vectors

One of the simplest and among the most important data types in R is the vector, which can be numerical or containing strings of characters. A simple way to build a vector is through the c function, which concatenates a series of data values, for example:

temperature = c(34, 45, 23, 29, 26, 31, 44, 32, 19, 22, 34)

in this case c concatenates a series of numerical data into a vector and the assignment operator = assigns it to the variable “temperature”, so that it can be retrieved later. Once the variable is created you can apply functions to it, for example

mean(temperature)

## [1] 30.81818

will compute the mean of the data vector. If you want to save the result of this function, you just have to assign it to another object:

mean_temp = mean(temperature)

note that in this case the value is assigned to the object mean_temp but it is not printed, you can display it with

print(mean_temp)

## [1] 30.81818

or for short, just calling the object

mean_temp

## [1] 30.81818

You can also perform simple arithmetic operations on a vector, for example:

temperature + 10

##  [1] 44 55 33 39 36 41 54 42 29 32 44

will add 10 to each element of the vector.

You can also build vectors of characters, quoting each element of the vector

color = c("blue", "green", "red" )

The length function is used to access the number of element present in a vector

length(color)

## [1] 3

3.2 Indexing vectors

It is possible to access only subsets of data in a vector and also assign them to another vector. The most basic form of indexing is based on the position of the data in the vector. For example, to access only the datum in the third position of a vector called temperature, you would simply type:

temperature[3]

## [1] 23

if you would like to access the data in more than one position of the vector, let’s say the first, the third and the sixth, you can again use the function concatenate inside the indexing command:

temperature[c(1, 3, 6)]

## [1] 34 23 31

to access the data from, say, the third position to the tenth position you can use:

temperature[3:10]

## [1] 23 29 26 31 44 32 19 22

and if you want to assign this subset to another vector called "white", you can just type:

white = temperature[3:10]

if you want to access all the vector but the first five positions:

temperature[-(1:5)]

## [1] 31 44 32 19 22 34

since in R there is not a “delete” command, you can use this form of subsetting to remove elements of a vector, for example, if you would like to cancel the fourth element of the temperature vector you would write:

temperature = temperature[-4]

Furthermore, to access subsets of data you can do much more magic using logical operators (see Table 3.1) and other tricks, for example if you want to access in a vector only the data greater than a certain value, you can use the > (greater than) logical operator:

temperature[temperature>30]

## [1] 34 45 31 44 32 34

In order to concatenate logical commands, you can use the & (and) logical operator:

temperature[temperature>30 & temperature<35]

## [1] 34 31 32 34

Table 3.1: Logical Operators.
Operator	Description
`&`	Intersection (“and”)
`&&`	“and” (lazy evaluation)
`\|`	Union (“or”)
`\|\|`	“or” (lazy evaluation)
`!`	Negation
`xor`	Exclusive “or”
`isTRUE(x)`

Table 3.2: Relational Operators.
Operator	Description
`<`	Less than
`<=`	Less than or equal to
`>`	Greater than
`>=`	Greater than or equal to
`==`	Equal to
`!=`	Not equal to

It is also possible to apply labels to the positions of a vector, and then access the datum in a given position through its label:

temperature = c(34, 45, 23, 29, 26)
names(temperature) = c("Johnny", "Jack", "Tony", "Pippo", "Linda")
temperature["Tony"]

## Tony 
##   23

3.2.1 The `seq` function

The seq function can be used to create evenly spaced sequences of numbers

seq(1,10)

##  [1]  1  2  3  4  5  6  7  8  9 10

the default increment is 1, but you can change it with the option by:

seq(1, 1.9, by=0.1)

##  [1] 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9

There’s a shortcut for sequences with an increment of 1

a = 1:10
a

##  [1]  1  2  3  4  5  6  7  8  9 10

3.2.2 The `rep` function

You can use the rep function to create vectors which contain repetitions of the same elements. Let’s start from the most simple use:

vector1 = rep(3, 13)

simply creates a vector of 13 elements, all having the value 3. More interestingly, you can repeat sequences of numbers:

rep(1:4, 3)

##  [1] 1 2 3 4 1 2 3 4 1 2 3 4

as you see the above command repeats the sequence 1,2,3,4 three times. Furthermore, you can also specify the number of times a given element of the sequence should be repeated:

rep(1:4, 3, each=2)

##  [1] 1 1 2 2 3 3 4 4 1 1 2 2 3 3 4 4 1 1 2 2 3 3 4 4

There are other ways to achieve this same effect, for example:

rep(rep(1:4, c(2, 2, 2, 2)), 3)

##  [1] 1 1 2 2 3 3 4 4 1 1 2 2 3 3 4 4 1 1 2 2 3 3 4 4

would yield the same effect.

Even if it can look pretty useless at first, the rep function comes in very handy for example, when you want to transform the data in a table from “one row per participant”, to “one row per observation”, which is necessary for example to run a repeated measures ANOVA with the aov function. rep makes it all easier as you can create vectors in which the occurrence of the levels of a factor are repeated over and over.

3.3 Matrix facilities

There are different ways for creating a matrix in R, you often start from a vector, and then transform it into a matrix with the matrix function:

matr = c(3, 5, 6, 2, 5, 7, 9, 1, 5, 4, 2, 3)
matr = matrix(matr, ncol=3, byrow=TRUE)
matr

##      [,1] [,2] [,3]
## [1,]    3    5    6
## [2,]    2    5    7
## [3,]    9    1    5
## [4,]    4    2    3

you give to the matrix function either the ncol or the nrow parameters to specify the layout of the matrix. The default method that R uses to fill in the matrix is by columns, so if you want to fill it by rows, you need to set true the option byrow, as in the example above.

Matrix indexing is similar to vector indexing:

matr[2,1]

## [1] 2

the first index refers to the row number, and the second index to the column number. Omitting one of the two indexes is useful for slicing, for example

matr[,2]

## [1] 5 5 1 2

gives all the rows in the second column. This could alternatively been written as

matr[1:4,2]

## [1] 5 5 1 2

where the index is a of rows. This notation is useful when you want to extract only part of the rows or columns, for example

matr[2:4,2]

## [1] 5 1 2

When the rows or columns to be extracted are not consecutive, you can use a vector of indexes for slicing

matr[c(2,4),2]

## [1] 5 2

To query the dimension of the matrix you can use the dim function, in this case our matrix has 4 rows and 3 columns:

dim(matr)

## [1] 4 3

The rows and columns of a matrix can also be assigned a name attribute through the dimnames function. The dimnames have to be a list of character vectors the same length as the matrix dimensions they refer to:

dimnames(matr) = list(c("row1", "row2", "row3", "row4"), c("col1", "col2", "col3"))
dimnames(matr) #dimnames is a list

## [[1]]
## [1] "row1" "row2" "row3" "row4"
## 
## [[2]]
## [1] "col1" "col2" "col3"

matr #now the matrix is printed with its dimnames

##      col1 col2 col3
## row1    3    5    6
## row2    2    5    7
## row3    9    1    5
## row4    4    2    3

the names of the rows can be retrieved with and the names of the columns with :

rownames(matr)

## [1] "row1" "row2" "row3" "row4"

colnames(matr)

## [1] "col1" "col2" "col3"

and these names can be indirectly used for sub-setting;

matr[1, which(colnames(matr) == 'col2')]

## [1] 5

3.3.1 Matrix operations

The function t gives the transpose of a matrix. The inverse of a matrix is obtained through the function solve. Some other operators are listed in Table 3.3). Example:

beta = solve(t(x)%*%x)%*%(t(x)%*%y)

Table 3.3: Matrix operations.
Operator	Function
`%*%`	Matrix multiplication
`det`	Determinant
`solve` I	nverse

3.4 Lists

Lists are objects that can contain elements of different modes (e.g numeric, character, logical), as well as other objects (vectors, matrices and also other lists). Let’s build a small list to see how we can work on it:

vec1 = 1:12
vec2 = c('w','h','m')
mylist = list(vec1, vec2)
mylist

## [[1]]
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12
## 
## [[2]]
## [1] "w" "h" "m"

The syntax for subsetting a list is a bit awkward (but as we’ll see later, naming the elements of a list makes things easier). To access an element of a list you can use the double brackets notation, for example

mylist[[1]]

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12

returns the first element of the list mylist, which is a vector of length 12, if you want to access, say, the third element of this vector, the syntax is as follows

mylist[[1]][3]

## [1] 3

Naming the elements of the list makes things easier

mylist=list(a=vec1, b=vec2)
mylist

## $a
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12
## 
## $b
## [1] "w" "h" "m"

now the first element of the list is named a, and the second b, and we can access them with a special “dollar sign” notation

mylist$a ## return element of the list named a

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12

mylist$a[1:3]

## [1] 1 2 3

It is also possible to use the double brackets notation with names

mylist[["a"]][3]

## [1] 3

To eliminate an element of a list, set it to NULL

vec1 = c(1, 2, 3)
vec2 = c("a", "b", "c")
myList = list(vec1=vec1, vec2=vec2)
myList

## $vec1
## [1] 1 2 3
## 
## $vec2
## [1] "a" "b" "c"

myList$vec1 = NULL
myList

## $vec2
## [1] "a" "b" "c"

note that this is different from eliminating an element of the vectors contained in the list, you can do the latter with

myList$vec2 = myList$vec2[-1]
myList

## $vec2
## [1] "b" "c"

3.5 Dataframes

Dataframes are one of the most important objects in R. You can think of it as a rectangular data structure, in which each column stores either the values of a numeric variable, or the levels of a factor, and each row represents an observation. Let’s look at an example, we’ll build a dataframe from 3 vectors, the first vector stores a variable, number of beers drunk during a week for twelve young people, the second is a factor vector, that specifies for each person whether he/she is a university student or not, so it has two levels, the third is also a factor vector, which tells the sex of each person, so it has two levels as well.

n_beers = c(6, 8, 4, 8, 9, 4, 5, 3, 4, 2, 3, 1)
occupation = rep(c("s", "w"), 6)
sex = c(rep("m", 6), rep("f", 6))
occupation = as.factor(occupation)
sex = as.factor(sex)

well, now let’s create the dataframe:

dats = data.frame(n_beers, occupation, sex)

it’s as simple as this, you have just put the three vectors together, let’s have a look at it

dats

##    n_beers occupation sex
## 1        6          s   m
## 2        8          w   m
## 3        4          s   m
## 4        8          w   m
## 5        9          s   m
## 6        4          w   m
## 7        5          s   f
## 8        3          w   f
## 9        4          s   f
## 10       2          w   f
## 11       3          s   f
## 12       1          w   f

as we said, each row holds the data of a single observation, in this case it corresponds to the data of a participant, but as we’ll see later, this is not always necessarily true. Each row gives a full specification for each observation, we know that the first participant drunk 6 beers, he’s a student, and he’s male, and we could tell the same data for the other participants. Since we have all this information, we could now compare for example the number of beers drunk by male vs females, or by male students vs female students. There are special functions to compute these values quickly like tapply and by (see 3.8.3), and other functions to get statistical tests, they will be dealt with as we go along.

3.5.1 Accessing parts of a dataframe

You can access, or refer to a column of a dataframe with the $ operator, in the example above suppose we removed all the original variables after creating the dataframe

rm(n_beers, occupation, sex)

we can’t now access them directly by name

mean(n_beers) #this will throw an object 'n_beers' not found error

we have to retrieve them from the dataframe

mean(dats$n_beers)

## [1] 4.75

the example might seem artificial (why did I remove them in the first place?), but very often you read in the data directly as a dataframe with the read.table function (see sec.~, so you’ll have to access them from the dataframe. Another option is to use the function attach, which attaches the dataframe to the path that R searches when evaluating a variable, in this way you don’t have to refer to the dataframe to access the values of a variable

attach(dats)
mean(n_beers)

## [1] 4.75

this is OK only if you’re working with a single dataframe, and you don’t want to manipulate the variables in it. In fact if you accidentally attach two dataframes that share some variable names, or you try to change an object of a dataframe after it has been attached, strange things may happen, you’ve been warned, the details are in the R manual. The function detach detaches the dataframe from the search path.

3.5.2 Changing the names of variables in a dataframe

Sometimes you might want to change the names of the variables in a dataframe, for example when you create new dataframes with the unstack function, or just because you don’t like the way you called it initially. You can visualise the names for the variables with the function names

names(dats)

## [1] "n_beers"    "occupation" "sex"

or if you want to see just the first one:

names(dats)[1]

## [1] "n_beers"

you can change it with a simple assignment:

names(dats)[1] = "beers"

or if you want to change more than one:

names(dats) = c("brs", "occ", "sx")

3.5.3 Other ways to subset a dataframe

A dataframe actually is just a special kind of list (a list of class dataframe), so we can use the normal list notation to subset dataframes

dats[[1]]

##  [1] 6 8 4 8 9 4 5 3 4 2 3 1

Sometimes it’s useful to think of a dataframe as a matrix, and use matrix notation for subsetting

dats[1,] ## extract first row, all columns

##   brs occ sx
## 1   6   s  m

dats[which(dats$n_beers>4),]  ## records for subjs who drink > 4 beers

## [1] brs occ sx 
## <0 rows> (or 0-length row.names)

3.6 Factors

Data Vectors can be made not only of numerical values or of strings, but also factors. Factor vectors are very similar to character vectors, and could be seen as character vectors with some special properties. A factor vector usually consists of two or more levels, and can be created with the factor function. For example, suppose we are studying the drinking habits of 6 individuals, and we have measured their alcohol consumption (in alcohol units) during a week:

alcoholUnits = c(7, 2, 15, 10, 1, 4)

the first three individuals are males, and the last three females and we can encode this information using a factor vector:

sex = factor(c("m", "m", "m", "f", "f", "f"))
sex

## [1] m m m f f f
## Levels: f m

as you can see a factor has a levels attribute that specifies the possible values the factor can assume, and by default it is given by the unique values the factor vector can assume, sorted in alphabetical order.

One important side effect of the levels attribute is that the way factor levels are ordered determines the sorting order of statistical summaries and graphics. For example, if we use the tapply function to calculate the average alcohol units consumption by sex:

tapply(alcoholUnits, list(sex), mean)

## f m 
## 5 8

the results for females are shown before the results for males. If we want the results for males to be presented before the results for females we can specify this ordering when creating the factor:

sex = factor(c("m", "m", "m", "f", "f", "f"), levels=c("m", "f"))
tapply(alcoholUnits, list(sex), mean)

## m f 
## 8 5

ordering the levels of a factor for display purposes should not be confused with the concept of an ordered factor.

3.6.1 Renaming the levels of a factor

To rename the levels of a factor we can use the labels argument to the factor function. Suppose that we have a sex factor coded as ‘f’ for females and ‘m’ for males:

sex = factor(c("m", "m", "m", "f", "f", "f"))

we can change the coding to ‘Male’ and ‘Female’ as follows:

sex = factor(sex, levels=c("f", "m"), labels=c("Female", "Male"))
sex

## [1] Male   Male   Male   Female Female Female
## Levels: Female Male

alternatively we can also use the levels function:

sex = factor(c("m", "m", "m", "f", "f", "f"))

currently the levels are c('f', 'm'):

levels(sex) #this gets the current levels

## [1] "f" "m"

we can change them with:

levels(sex) = c("Female", "Male") #this sets the levels

we can also change just the name of one of the levels if we want to:

sex = factor(c("m", "m", "m", "f", "f", "f")) #original factor
levels(sex)[which(levels(sex) == "m")] = "Male"
sex

## [1] Male Male Male f    f    f   
## Levels: f Male

3.6.2 Creating factors with `gl`

A handy function for creating factors for data with a regular pattern of factor levels is gl:

sex = gl(2, 3, label=c("male", "female"), length=6)
sex

## [1] male   male   male   female female female
## Levels: male female

the first argument to the function specifies the number of levels, and the second argument the number of consecutive repetitions of each level, the pattern is repeated up to the number of elements specified by the length argument. Note the different pattern created when the number of consecutive repetitions is set to 1 and the total length is left unchanged:

sex = gl(2, 1, label=c("male", "female"), length=6)
sex

## [1] male   female male   female male   female
## Levels: male female

3.6.3 Natural sort order for character and factor vectors

It’s common to assign identifiers to participants in an experiment as:

ids = c("P1", "P2", "P3", "P4", "P5", "P6","P7", "P8", "P9", "P10", "P11")

when you use these identifiers for summarizing or plotting data as a function of participant id R will sort the output in strict alphabetical order, which is equivalent to the output of this function:

sort(ids)

##  [1] "P1"  "P10" "P11" "P2"  "P3"  "P4"  "P5"  "P6"  "P7"  "P8"  "P9"

often what you want instead is a natural sort order, in which P10 comes after P9 and not after P1. To force R to use a natural sort order you can use a factor vector and sort the factor levels using the mixedsort function in the package gtools:

library(gtools)
fids = factor(ids, levels=mixedsort(levels(ids)))
sort(fids)

## factor(0)
## Levels:

3.7 Getting info on R objects

The most useful function to summarise information about many R object is str:

a = seq(0, 10, .1)
str(a)

##  num [1:101] 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 ...

b = c("a", "b", "c")
str(b)

##  chr [1:3] "a" "b" "c"

in the example shown str gives information on the storage mode of the two vectors, numeric for a and character for b, it also gives information on the number of elements present and on the shape of the array (compare the output of str for a vector and a matrix). str gives also useful compact summaries of the contents of lists, including nested lists.

Another useful function is mode, which gives the storage mode of an R object:

mode(a)

## [1] "numeric"

mode(b)

## [1] "character"

3.8 Changing the format of your data

In general statistical software require your data to be entered in a specific format in order to perform statistical analyses on them, and R is no exception. R provides many powerful functions to change the format of your data if they happen to be in a format that is not suitable for applying a given statistical function on them. The process of changing the format of your data with these functions might seem very complicated at first, however you should keep in mind the following things:

You don’t really need to learn all of the functions that R provides to manipulate your data and change their format. Once you learn a procedure that does the job you can stick with it and you’ll be fine most of the times.
Once you understand the “logic” and the structure of the data format that R expects to apply some statistical functions, changing the layout of your data to match this structure will be easy. Moreover, the data format that R wants is most of the times one and only one: The “one row per observation format”, which will be explained below.
In this tutorial you will see different examples in which the format of the data, stored in a given file don’t match the format R wants. This is just for illustrative purposes. In real life if you’re doing a research or an experiment, you can often gather your data in a format that is already suitable for performing statistical analyses.
You don’t really have to use R to change the layout of your data if you don’t like the functions it provides to do this job. You can always use some external programs to achieve the same results, for example spreadsheets programs such as Libreoffice Calc. What’s really important is that you understand the structure of the format the R expects.

This said, I would advice you to learn some of the functions that R provides to rearrange your data for at least two reasons: 1) They’re very powerful and can actually save you time once you learn them, and 2) many examples in this tutorial and in other books use them, so you’ll often need to know them to understand what’s going on :)

3.8.1 The “one row per observation” (long) format

While statistic textbooks and scientific articles often show data in a “wide” format that is suitable and immediate for the “human eye”, like the one shown in Table 3.4, statistical software often don’t quite like it and would rather have the same data rearranged in a “long” format, as shown in Table 3.5.

Table 3.4: Data format suitable for the “human eye”.
Group A	Group B	Group C
5	4	7
2	4	5
3	5	7
4	5	8
6	4	7

Table 3.5: Data format suitable for R.
Value	Group
5	A
2	A
3	A
4	A
6	A
4	B
4	B
5	B
5	B
4	B
7	C
5	C
7	C
8	C
7	C

The main difference is that while in the first format you have more than one observation in the same row, and you can identify the group to which each observation belongs to through the column headers (“Group A”, “Group B” and “Group C”), in the second format you have only one observation for each row. This observation is then fully identified with a “label” that appears in the second column. A better way to describe the second column is to say that in the above case “Group” is a factor, and “A”, “B” and “C” define the levels of this factor for each group.

You could also be running an experiment in which you manipulate more than one factor. For example you might have two groups, “Patients” and “Controls”, which are tested under two conditions: condition “1” and condition “2”. In this case you might display your data as shown in Table 3.6 to make them easily readable to humans. However for analyzing your data with R you would need to reshape the data as shown in Table 3.7, with one column specifying the group, and another column specifying the condition for a given observation.

Table 3.6: Data format suitable for the “human eye” with more than one factor.
Patients Condition1	Patients Condition 2	Controls Condition 1	Controls Condition 2
7	6	6	4
5 4	5	2
8 7	7	4
8 8	6	5
6 5	5	3

Table 3.7: Data format suitable for R with more than one factor.
Value	Group	Condition
7	P	1
5	P	1
8	P	1
8	P	1
6	P	1
6	P	2
4	P	2
7	P	2
8	P	2
5	P	2
6	C	1
5	C	1
7	C	1
6	C	1
5	C	1
4	C	2
2	C	2
4	C	2
5	C	2
3	C	2

Finally, you might be running an experiment with a repeated measures design, in which all participants are exposed to all the levels of the within subjects factors. For example you might have your participants recall word lists either under the effects of a drug or not (factor 1) and with words concrete or abstract words (factor 2). In this case the data for presentation might look like the ones in Table 3.8, in which each row represents a single participant. Again for R you need to rearrange the data so that each row represents a single observation, and in the case of a repeated measures design you need to add another column that identifies the levels of the “participants” factor as shown in Table 3.9

Table 3.8: Data format suitable for the “human eye” in a repeated measures design.
Drug Concrete	Drug Abstract	No-Drug Concrete	No-Drug Abstract
7	6	6	4
5	4	5	2
8	7	7	4
8	8	6	5
6	5	5	3

Table 3.9: Data Format Suitable for R, repeated measures design.
Value	Drug Exposure	Word Type	Participant
7	D	C	1
5	D	C	2
8	D	C	3
8	D	C	4
6	D	C	5
6	D	A	1
4	D	A	2
7	D	A	3
8	D	A	4
5	D	A	5
6	N	C	1
5	N	C	2
7	N	C	3
6	N	C	4
5	N	C	5
4	N	A	1
2	N	A	2
4	N	A	3
5	N	A	4
3	N	A	5

3.8.2 The `stack` and `unstack` functions

One of the utilities provided by R to manipulate the format of your data is the stack function. If you have your data in a dataframe with a layout similar to that shown in Table 3.4, you can use the stack function to get a “one row per observation” format. What the stack function does is to create a single long vector from the vectors you have in your dataframe, and an additional factor vector which identifies the level for each observation. Here’s an example, the data are in the file stack.txt:

dats = read.table("stack.txt", header=TRUE)

this creates the dataframe

dats = stack(dats)

this reshapes the dataframe into a “one row per observation” form.

Please note that R assigns names to the vectors in the new dataframe, you can see them in the header of the dataframe, you might need to know them for successive operations.

The unstack function simply does the opposite of the stack function, and you can use it if you want to switch back to your original dataframe format.

dats = unstack(dats)

The unstack function can do more tricks, if you have a dataframe with one observation per row, a column with a response variable, and two or more factor columns, you can unstack the values of the response variable according to the levels of only one factors or according to the levels of two or more factors. Suppose lat is your response variable, and you have two factors, congr with 3 levels and isi, also with 3 levels. The command:

dats = unstack(dats, form=lat~congr)

unstack the values of the response variable according to the levels of the congr factor, thus creating 3 columns, one for each level.

The command:

dats = unstackd(ats,form=lat~congr:isi)

unstacks the values of the response variable according to the levels of both factors, thus creating $3x3= 9$ columns, the first column contains the values at level 1 of congr and level 1 of isi, the second one contains the values at level 1 of congr and level 2 of isi, and so on for all the possible combinations.

3.8.3 The `tapply` and `aggregate` functions

The tapply function allows you to extract information from a dataframe, for example the mean or standard deviation of a given variable on the bases of one or more factor. The function name is related to the fact that it is used to apply a function (e.g. the mean) to a subsets of the dataframe chosen on the basis of one or more factors. We’ll use the InsectSprays dataset to illustrate the use of tapply. The dataset contains the number of insects still alive in agricultural experimental units treated with six different types of pesticide.

data(InsectSprays)
head(InsectSprays)

##   count spray
## 1    10     A
## 2     7     A
## 3    20     A
## 4    14     A
## 5    14     A
## 6    12     A

meanSpray = tapply(X=InsectSprays$count,
                  INDEX=InsectSprays$spray,
                  FUN=mean)
meanSpray

##         A         B         C         D         E         F 
## 14.500000 15.333333  2.083333  4.916667  3.500000 16.666667

the arguments to tapply are X, the column of the dataframe to which the function should be applied, INDEX, the factor used for subsetting the dataframe, and FUN, the function to be applied. The function returns an array, in this case a vector, but can be a matrix, or multi-dimensional array. The INDEX argument indeed can be a list of factors, in this case the function chosen is applied to group of values given by a unique combination of the levels of these factors. We’ll see an example by modifying the InsectSprays dataset including another fictitious factor. The new factor will be the season in which the fields were sprayed. The values will be returned in a matrix.

season = gl(4, 3, 72, labels=c("winter", "spring",
                                 "summer", "autumn"))
Ins = data.frame(InsectSprays, season)
meanSpray = tapply(X=Ins$count,
                   INDEX=list(Ins$spray, Ins$season),
                   FUN=mean)
meanSpray

##      winter    spring    summer    autumn
## A 12.333333 13.333333 16.666667 15.666667
## B 16.333333 13.666667 17.666667 13.666667
## C  2.666667  2.000000  2.000000  1.666667
## D  6.666667  4.333333  5.000000  3.666667
## E  3.666667  4.666667  1.666667  4.000000
## F 11.666667 17.666667 16.333333 21.000000

The tapply is often very useful, for example, after having calculated the means in this way, it is very easy to visualise the data with a barplot

barplot(meanSpray, beside=TRUE, legend=T)

The aggregate function is very similar to tapply, but rather than returning an array, it returns a dataframe, which can be useful in some situations.

InsDf = aggregate(x=Ins$count,
                  by=list(sprayType=Ins$spray, season=Ins$season),
                  FUN=mean)
InsDf

##    sprayType season         x
## 1          A winter 12.333333
## 2          B winter 16.333333
## 3          C winter  2.666667
## 4          D winter  6.666667
## 5          E winter  3.666667
## 6          F winter 11.666667
## 7          A spring 13.333333
## 8          B spring 13.666667
## 9          C spring  2.000000
## 10         D spring  4.333333
## 11         E spring  4.666667
## 12         F spring 17.666667
## 13         A summer 16.666667
## 14         B summer 17.666667
## 15         C summer  2.000000
## 16         D summer  5.000000
## 17         E summer  1.666667
## 18         F summer 16.333333
## 19         A autumn 15.666667
## 20         B autumn 13.666667
## 21         C autumn  1.666667
## 22         D autumn  3.666667
## 23         E autumn  4.000000
## 24         F autumn 21.000000

if you don’t give a name to the grouping factors as we did with SprayType=Ins$spray a default name will be given. One slightly annoying thing is that, as far as I know, it is not possible to assign a name to the resulting variable (it will just be named x). However it can be changed afterwards, here’s a solution that should work whatever the number of factors in the dataframe:

names(InsDf)

## [1] "sprayType" "season"    "x"

names(InsDf)[which(names(InsDf)=="x")] = "count"
names(InsDf)

## [1] "sprayType" "season"    "count"

3.9 The `scale` function

The scale function can be used to easily transform your data into $z$ scores. Here’s a trivial example:

a = c(1, 2, 3)
scale(a)

##      [,1]
## [1,]   -1
## [2,]    0
## [3,]    1
## attr(,"scaled:center")
## [1] 2
## attr(,"scaled:scale")
## [1] 1

3.10 Printing out data on the console

As you probably have already noted, after you’ve created a data object, just typing its name on the console and pressing Enter will display the values it contains. Sometimes however, you might want to see only part of the data, for example to do some checking, or because the data object is too big and it’s not printed nicely on the console. The functions head and tail let you look only at the first or the last part of your data respectively. For example, let’s load the iris dataset in the datasets package, the command:

library(datasets)
head(iris)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

will print only the first 6 observations. You can visualise more (or less) than 6 observations by setting the n option:

head(iris, n=10)

##    Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1           5.1         3.5          1.4         0.2  setosa
## 2           4.9         3.0          1.4         0.2  setosa
## 3           4.7         3.2          1.3         0.2  setosa
## 4           4.6         3.1          1.5         0.2  setosa
## 5           5.0         3.6          1.4         0.2  setosa
## 6           5.4         3.9          1.7         0.4  setosa
## 7           4.6         3.4          1.4         0.3  setosa
## 8           5.0         3.4          1.5         0.2  setosa
## 9           4.4         2.9          1.4         0.2  setosa
## 10          4.9         3.1          1.5         0.1  setosa

using tail will show the last rows of the dataframe, and again you can instruct the function to show more or less rows by passing the n argument:

tail(iris, n=2)

##     Sepal.Length Sepal.Width Petal.Length Petal.Width   Species
## 149          6.2         3.4          5.4         2.3 virginica
## 150          5.9         3.0          5.1         1.8 virginica

A data structure that is a modern take on dataframes, the tibble, will be described in Chapter 12. Tibble printouts by default only show the rows and columns that fit on the screen (a default which I find annoying). See Section 12.1 for instructions on how to override this default if you’re using tibbles and don’t like their default print behavior.

3.10.1 Reading numbers in exponential notation

Often R prints out numbers in exponential notation. In order to understand exponential notation it’s first necessary to introduce scientific notation.

A number in scientific notation is in the form $a\cdot 10^b$, for example 300 could be written in scientific notation as $3\cdot 10^2$. The components of a number in scientific notation are also named as $mantissa \cdot 10^{characteristic}$. Remember that a number with a negative exponent, for example $10^{-2}$ can be rewritten as \[10^{-2}= \frac{1}{10^2}=0.01\] so, for example, $0.003$ can be rewritten in scientific notation as $3\cdot 10^{-3}$, because \[3\cdot 10^{-3}= 3\cdot \frac{1}{10^3}= 0.003\]

R, as most calculators doesn’t actually use scientific notation, it uses instead exponential notation. The exponential notation is a shorthand version of the scientific notation, in which, for example, $10^3$ is replaced by $e3$, where $e$ stands for exponent. So in our previous examples 300 would be written as $3e2$ and 0.003 would be written as $3e3$. Below are a few conversion examples.

Table 3.10: Number Formats.
Number	Scientific Notation	Exponential Notation
$10$	$1\cdot 10^1$	$1e1$
$20$	$2\cdot 10^1$	$2e1$
$200$	$2\cdot 10^2$	$2e2$
$350$	$3.5\cdot 10^2$	$3.5e2$
$0.00353$	$3.53\cdot 10^-3$	$3.53e-3$

As a quick and dirty rule, remember that when you’re multiplying a number by $10^{exponent}$, as you add to the exponent, you’re adding a 0 to the number, or shifting the point by one position towards the right if it’s a decimal number. As you subtract to the exponent, you’re deleting a 0 from the number, or shifting the point by one position towards the left.

3.11 Creating and editing data objects through a visual interface

If you want to use a visual interface for creating a dataframe, first create an empty dataframe with:

mydataframe = data.frame()

then you can call a spreadsheet like editor to fill in the dataframe with:

data.entry(mydataframe)

fix(mydataframe)

If the data object is a vector, fix will call a text editor to edit the object instead of the spreadsheet like interface, so if you want the latter, use the function data.entry instead. However, using a simple text editor for fixing a vector might be more practical, if you want to use a different text editor from the one that fix calls by default, you can change the editor option:

fix(myvector, editor="emacs")

or just call the editor on the object:

emacs(myvector)

On Windows you could try:

fix(myvector, editor="notepad")

4 R programming

4.1 Control structures

4.1.1 Conditionals

4.1.1.1 If..else conditional execution

It is possible to insert and execute control structures directly from the R interpreter, but for the following examples, I’ll assume you’re writing the commands to a batch file, and then executing them through the source() command.

The general form of conditional execution in R is:

  if (cond){
    do_this
   } else {
     do_something_else
   }

here’s a trivial example:

money = 1300
if (money > 1200){
    print("good!")
} else {
    print("troubles...")
}

## [1] "good!"

it’s important that the else statement is on the same line where the previous command ends (in the above example that’s the closing brace on the fourth line), otherwise the interpreter sees it as unrelated to the previous if and will give an error (the if statement could also be used by itself, so it would be seen as a complete statement if else does not appear on the same line).

It is also possible to execute more than one command upon the fulfilment of a given condition:

money = 900
expenses=1200
if (money > expenses){
    print("good!")
    shopping= money-expenses
} else {
    print("troubles...")
    shopping=NA
}

## [1] "troubles..."

print("Money available for shopping:")

## [1] "Money available for shopping:"

print(shopping)

## [1] NA

Finally it is possible to add branches to your control structure with the else if statement:

expenses = 1000
laptop  = 1000
if ((money-expenses) > 1000){
    print("great!! buy new laptop")
    shopping=(money-expenses)-laptop
} else if ((money-expenses) > 0 && (money-expenses) <= 1000){
    print("no laptop, just shopping and save some")
    shopping= (money-expenses)/2
} else {
    print("troubles...")
    shopping=NA
}

## [1] "troubles..."

print("Money available for shopping:")

## [1] "Money available for shopping:"

print(shopping)

## [1] NA

4.1.1.2 `ifelse`

The ifelse function is handy for testing all the elements of a vector on a given condition, the general form is:

  ifelse(condition, value_if_cond_true, value_if_cond_false)

for example, let’s say we want to categorise the results of a classroom test, scored from 1 to 10 as “pass” if the score was equal to, or greater than 6 and “fail” if the score was less than 6:

score = c(4,7,6,5,8,6,7)
admission = ifelse(score >= 6, "pass", "fail")
admission

## [1] "fail" "pass" "pass" "fail" "pass" "pass" "pass"

so, the first argument of the ifelse function, is the condition that we want to test, the second argument is the value that should be returned if the condition is met, and the third argument is the value that should be returned if it is not.

4.1.1.3 `xor`

The function xor implements the exclusive logical “or” operator, that is, it evaluates to TRUE if exclusively one of two alternative conditions is met, otherwise, it evaluates to false. The latter occurs both, when none of the conditions is met and when both are met simultaneously.

a=6
xor(a>5, a>7)

## [1] TRUE

xor(a>5, a>3)

## [1] FALSE

in the first example, only the first condition (a>5) is met, so the function evaluates to true. In the second example, both conditions are satisfied, but since we’re using xor and you can have one thing or the other, but not both together, the function evaluates to false.

## [1] 6

a=a[-which(a>5)]

4.1.2 Loops

4.1.2.1 `for` loops

for loops can be used to iterate over elements of a vector:

for (i in 1:4){
    print(i)
}

## [1] 1
## [1] 2
## [1] 3
## [1] 4

in the above case the vector is given by the sequence of numbers 1:4. The following example uses a vector consisting of a sequence of letters:

letts = c("a", "b", "c", "d")
for (ltt in letts){
    print(ltt)
}

## [1] "a"
## [1] "b"
## [1] "c"
## [1] "d"

for loops can iterate also over elements of a list:

lst = list(a=c(1, 8), b=c(2, 7), c=c(3, -4))
for (itm in lst){
    print(itm[2])
}

## [1] 8
## [1] 7
## [1] -4

for loops can be nested at will:

for (ltt in letts){
    for (i in 1:4){
        print(paste0(ltt, " - ", i))
    }
}

## [1] "a - 1"
## [1] "a - 2"
## [1] "a - 3"
## [1] "a - 4"
## [1] "b - 1"
## [1] "b - 2"
## [1] "b - 3"
## [1] "b - 4"
## [1] "c - 1"
## [1] "c - 2"
## [1] "c - 3"
## [1] "c - 4"
## [1] "d - 1"
## [1] "d - 2"
## [1] "d - 3"
## [1] "d - 4"

4.1.2.2 `while` loops

while loops continue until a certain condition is met:

i = 1
while (i<4){
    print(i)
    i = i+1
}

## [1] 1
## [1] 2
## [1] 3

4.2 Functions

Functions are one of the fundamental building blocks of programming. While using R we call functions all the time, but why write new ones? A major reason is to make your analysis code more modular, readable, compact, and reusable. Whenever you’re repeatedly performing a series of operations on well-defined inputs and outputs in your analyses scripts you should consider “packaging” those operations into functions. The syntax for declaring a function is:

my_func = function(arg1, arg2){
    ## function code here
}

where my_func is the name of the function, and arg1, arg2 are the arguments we want to pass to the function. For example let’s define a function that computes the root mean square (RMS) of a vector:

RMS = function(vls){
    RMS_val = sqrt(mean(vls^2))

    return(RMS_val)
}

the last line indicates the value returned by the function, if no explicit return statement is provided, the function will return the value of the last evaluated expression. We can now run the function:

RMS(c(-2, 5, -8, 9, -4))

## [1] 6.164414

Let’s suppose now that we want our RMS function to handle the possibility of missing values in the input vector. If there are one or more NA the RMS function, as is defined right now, will return NA:

RMS(c(-2, 5, -8, 9, NA))

## [1] NA

we want this to be the default behavior, but we want to give users the option to ignore the missing values and compute the RMS of the subset of remaining values. We can do this by defining the RMS function as follows:

RMS = function(vls, na.rm=FALSE){
    if (na.rm == TRUE){
        vls = vls[is.na(vls) == FALSE]
    }
    RMS_val = sqrt(mean(vls^2))

    return(RMS_val)
}

running the function with the default value for na.rm still gives the same result as before:

RMS(c(-2, 5, -8, 9, NA))

## [1] NA

specifying na.rm = TRUE, instead, computes the RMS of the non-missing values

RMS(c(-2, 5, -8, 9, NA), na.rm=TRUE)

## [1] 6.595453

4.3 String processing

One of the strengths of R, in my opinion, lies in the way it deals with character strings. Certain objects, for example dataframes, allow to mix strings with other data types, subsets of certain objects (again dataframes are an example, but also lists), can be easily given meaningful names and retrieved. This adds much flexibility and ease of use to R compared to other languages (e.g. MATLAB). One aspect that is perhaps less known however, are the powerful string processing functions that R gives you. Once you get to know them you’ll realise you can do all your data analysis in R, without the need to use other languages, like python or perl for pre-processing.

The simplest thing you can do with a string, is counting its characters, which you can do with the nchar function:

my_string = 'I love R'
nchar(my_string)

## [1] 8

The second thing you can do with strings is extracting parts of them. There are various way to achieve this. Two of the most useful functions are substr and strsplit.

substring, as the name suggests, returns part of a string:

substr(my_string, start=1, stop=4)

## [1] "I lo"

if you want to get a portion of a string from some point in the middle, to the end:

substr(my_string, start=5, stop=nchar(my_string))

## [1] "ve R"

substr can be also used to replace parts of a string

substr(my_string,start=1,stop=3)='qqq'
my_string

## [1] "qqqove R"

4.3.1 Using regular expressions

b=c('the','atheist','theme','therion','thin','jjthe')   
grep('^the',b,value=TRUE) ## match only when pattern appears at the beginning

## [1] "the"     "theme"   "therion"

grep('the$',b,value=TRUE) ## match only when pattern appears at the end

## [1] "the"   "jjthe"

grep('^the$',b,value=T) ## match exactly 'the' not followed or preceded by anything

## [1] "the"

grep('the[i,m]',b,value=TRUE)## match 'the' followed by 'i' or 'm'

## [1] "atheist" "theme"

grep('the[^i]',b,value=TRUE)## match 'the' followed by anything except 'i'

## [1] "theme"   "therion"

grep('the.',b,value=TRUE)## match 'the' followed by anything

## [1] "atheist" "theme"   "therion"

grep('.the',b,value=TRUE)## match 'the' preceded by anything

## [1] "atheist" "jjthe"

glob2rx translates a wildcard pattern, as used in most shells (for example for listing files with the Unix ls), in a regular expression, so if you’re used to wildcards this comes is handy

glob2rx('the*')

## [1] "^the"

glob2rx('the')

## [1] "^the$"

4.4 Tips and tricks

4.4.1 Convert a string into a command

cmd = "vec = c(1,2,3)"
eval(parse(text=cmd))

4.5 Creating simple R packages

If you start writing your own functions and you use them often, probably you will soon get tired of sourcing the files containing each function to make them available at each session. There are at least two ways around this problem:

put all your function files in a directory and write a function that systematically sources them all.
build a R package

The first solution is rather simple, give the .R extension to your R function files and put them in a directory. Although there is not a built-in function to source all the R files present in a directory, the documentation for the source function gives an example on how to do it (see ?source):

  ## If you want to source() a bunch of files, something like
  ## the following may be useful:
  sourceDir = function(path, trace = TRUE, ...) {
    for (nm in list.files(path, pattern = "\\.[RrSsQq]$")) {
      if(trace) cat(nm,":")           
      source(file.path(path, nm), ...)
      if(trace) cat("\n")
    }
  }

the function sources all the files with the .R extension found in the directory indicated by the path argument. You can copy this function to a file, let’s say sourceDir.R, put it in your HOME directory and source it in your .First function in .Rprofile (see Section 17.1 for details the .First function and the .Rprofile file)

  ## This goes in .Rprofile in ~/
  .First = function(){
     source("~/sourceDir.R")
  }

now each time you call sourceDir with a directory as an argument, you will have all the functions defined there available. If you want them available at the beginning of each session, just add a call to sourceDir for the directories you want to add in your .First function as well. So for example, if your R function files are in the directory myRfunctions, add the following to your .First function:

  ## This goes in .Rprofile in ~/
  .First = function(){
     source("~/sourceDir.R")
     sourceDir("~/myRfunctions")
  }

Building a R package requires a bit more work. The detailed documentation for doing this is provided in the Writing R Extensions manual available at the CRAN website http://cran.r-project.org/. That documentation looks at best daunting for a beginner, indeed writing a R package is not trivial, however if all you have is pure R code, and you just want to build a simple package for your own use, the task should not be too difficult to achieve. A very useful document is An introduction to the R package mechanism, it can be found at the following URL http://biosun1.harvard.edu/courses/individual/bio271/lectures/L6/Rpkg.pdf. In the following sections I’ll try to explain how to build a simple R package, much of what I say is drawn from the above cited documents.

4.5.1 The bare minimum to create a package

The quickest way to get started is to use the function package.skeleton to create the first ``draft’’ of your package. Start a R session, make sure that there are not R objects in your session, otherwise they will be bundled in your package

rm(list=ls(all=TRUE))

now source all the function files you want to include in your package, for example

source("/home/sam/myFunctions.R")
source("/home/sam/soundFunctions.R")

and the call the package.skeleton function with the name you want to give to your package as the argument, for example ``mypkg’’

package.skeleton("mypkg")

this will create a directory called mypkg with two sub-directories, R containing your code, and man containing the documentation files. Furthermore a file called DESCRIPTION will be created. If the objects you are packaging include datasets, a data directory will also be created. These are the essential elements needed to build a package. The exact content of these files and directories, and how to edit them will be explained later, for the moment I’ll give an overview of the steps required to start using your package. The next step consists of building the package. Start a shell (not a R session), move one directory above the mypkg directory we’ve just created and give the command

$ R CMD build mypkg

to build the package, this will create a tar gzipped file with everything necessary to install the package, the next step to do is indeed the installation. I would recommend installing your own packages in a separate directory from the default package installation directory, let’s say ~/personalRLibrary, to install the package in this directory, still from the shell call

$ R CMD INSTALL -l ~/personalRLibrary nameOfTarFile.tar.gz

now from a R session you can call your package with

library(mypkg, lib="~/personalRLibrary")

if you want to add permanently your personal R library to the library search path, you can add the following line to the .First function in your .Rprofile

## This goes in .Rprofile in ~/
.First = function(){
    .libPaths(c((.libPaths()), "~/personalRLibrary/"))
}

in this way, after starting a new session you’ll be able to load your package without having to specify in which library it is located

   library(mypkg)

The one described above is a very quick but rough way of creating a package, in order to properly create a R package a number of additional steps, like writing the documentation, and adding examples, need to be followed. Some of these steps will be described in the following sections. Always remember that a very useful thing to do when learning how to build a package is to download some source packages and explore their contents.

4.5.1.1 Editing the `DESCRIPTION` file

The DESCRIPTION file follows the Debian control format, and has a key-value pair syntax. The default fields created by package.skeleton are pretty much self-explanatory. Other fields that can be added are

Depends If your package depends on a particular version of R, or on other packages, these should be listed here. For example:

  Depends: R (>= 1.9.0), gtools, gdata, stats

URL The URL of a website where you can find out mode about the package. For example:

URL: http://www.example.com

4.5.1.2 Editing the documentation

The documentation files reside in the man directory of your package. There is one documentation file for each function or data set present in the package. The documentation files are written in a like format called Rd. package.skeleton creates a skeleton of the documentation file, which just needs to be edited, the default fields are pretty much self-explanatory. For a more detailed explanation you can read the Writing R Extensions manual http://cran.r-project.org/doc/manuals/R-exts.html. I’ll give you just a few tips:

It is possible to add additional sections beside the default ones, for example it may be useful to add a ``Warnings’’ section if you have any warnings to give on the use of the function

\section{Warning}{Calling this function with arguments foo foo2 can cause ...}

In the seealso section, you can refer to other functions contained in your package, for example

\code{\link{functionFoo}}

will automagically add a hyperlink to the documentation for the function functionFoo

In the Examples section, you write code as if you were writing it in a R script. You can use datasets from your own package, or from the standard R dataset. Keep in mind that the examples should be directly executable by the user, either through copy and paste, or through the example() function. When the package is installed, the examples will appear in a directory called R-ex, however you do not need to bother about this, the R code for your examples needs to be written within the documentation Rd files.

The documentation requires the presence of one or more standard keywords. One way to get a list of these keywords is to download the tarball with the R sources, after unpacking it, you can find the keywords in a file within the doc directory called KEYWORDS.db.

4.5.1.3 Converting Rd files to other formats

HTML and LaTeX versions of the documentation files are automatically produced in the package installation process, you can find them in the html and latex directories of your package installation directory, respectively. You can also produce a single pdf or dvi file containing all the documentation using the following command from a shell

$ ## produce dvi
$ R CMD Rd2dvi /path/to/your/package/sources/
$ ## produce pdf
$ R CMD Rd2dvi --pdf /path/to/your/package/sources/

4.5.1.4 Adding additional function or data files to the package

Adding additional function files is quite straightforward, the files contained in the R sub-directory of your package directory are plain R files, so you can just write your functions, drop the files with your functions there, and next time you build the package the new functions will be included. The function prompt can be used to build the documentation templates for new functions:

myfun = function(arg){val = arg + 3}
prompt(myfun)

this will create a .Rd file which you can edit, and drop in the man directory.

Datasets can be saved using the save function:

mydata = seq(1, 10, .1)
save(mydata, file='mydata.rda')

documentation again can be produced using the prompt function

prompt(mydata)

4.5.1.5 Checking the package

The sanity check for the package can be done by issuing the following command from a shell

$ R CMD check /path/to/your/package/sources/

4.5.1.6 Other resources

Wickham (2015) is a book dedicated to the development of R packages. The draft of the 2 edition of the book is available here.

5 File input/output

5.1 Reading in data from a file

5.1.1 The `read.table` function

If the data are in a table-like format, with each row corresponding to an observation or a single case, and each column to a variable, the most convenient function to load them in R is read.table. This function reads in the data file as a dataframe. For example the data in the data file ratsData.txt that contain information (height, weight, and species) of 6 rats can be easily read in with the following command:

ratsData = read.table(file="datasets/ratsData.txt", header=TRUE)
ratsData

##   identifier height weight species
## 1       sa01    3.2    300       A
## 2       sa02    2.6    246       A
## 3       sa03    2.9    317       A
## 4       sb01    2.4    229       B
## 5       sb02    2.5    230       B
## 6       sb03    2.4    245       B

in this case we’ve set the option header=TRUE because the file contains a header on the first line with the variable names.

5.1.2 `scan`

Another very handy function for reading in data is scan, it can easily read in both tabular data in which all the columns are of the same type, or they are of different type, as long as they follow a regular pattern. We’ll read in the ratsData.txt file as an example:

x = scan(file="datasets/ratsData.txt", what=list(identifier=character(),
          height=numeric(), weight=numeric(), species=character()),
          skip=1)
str(x)

## List of 4
##  $ identifier: chr [1:6] "sa01" "sa02" "sa03" "sb01" ...
##  $ height    : num [1:6] 3.2 2.6 2.9 2.4 2.5 2.4
##  $ weight    : num [1:6] 300 246 317 229 230 245
##  $ species   : chr [1:6] "A" "A" "A" "B" ...

the what argument tells the scan function the mode (numeric, character, etc…) of the elements to be read in, if what is a list of modes, then each corresponds to a column in the data file. So in the above example we have the first column, the variable identifier, which is of character mode, the second column, height is of numeric mode, like the third column, weight, while the last column, species is of character mode again. Notice that we’re telling scan to skip the first line of the file (skip=1) because it contains the header. The object returned by scan in this case is a list, we can get the single elements of the list, corresponding to each column of the data file, with the usual methods for lists:

x[[1]] #first item in list (first column in file)

## [1] "sa01" "sa02" "sa03" "sb01" "sb02" "sb03"

x[["weight"]] #item named weight in list (third column in file)

## [1] 300 246 317 229 230 245

scan can do much more than what was shown in this example, like specifying the separator between the fields of the data file (comma, tabs, or whatever else, defaults to blank space), or specifying the maximum number of lines to be read, see ?scan for more details. I’ll present just another simple example in which we’ll read in a file whose data are all numeric. The file is rts.txt

x = scan("datasets/rts.txt", what=numeric())
str(x)

##  num [1:36] 0.12 0.132 0.102 0.096 0.103 0.087 0.113 0.134 0.109 0.132 ...

in this case the object returned is a long vector of the same mode as the what argument, a numeric vector. The file is however organised into three columns, which represent three different numeric variables. It is easy to reorganise our vector to reflect the structure of our data:

nRows = length(x)/3
xm = matrix(x, nrow=nRows, byrow=TRUE)

so we’ve got a matrix with the 3 columns of data originally found in the file, turning it into a dataframe would be equally easy at this point

xd = as.data.frame(xm)

However also in this case it is possible to simply read in each column of the file as the element of a list:

x = scan("datasets/rts.txt", what=list(v1=numeric(),
          v2=numeric(), v3=numeric()))
str(x)

## List of 3
##  $ v1: num [1:12] 0.12 0.096 0.113 0.132 0.124 0.105 0.109 0.143 0.127 0.098 ...
##  $ v2: num [1:12] 0.132 0.103 0.134 0.147 0.139 0.115 0.129 0.15 0.145 0.117 ...
##  $ v3: num [1:12] 0.102 0.087 0.109 0.123 0.124 0.102 0.097 0.119 0.113 0.092 ...

5.1.3 Low-level file input

Sometimes the file to be read is not nicely organised into separate columns each representing a variable, in this case the function readLines can either read-in the file as a character vector, in which each element is a line from the file. The lines can then be further processed to extract the data (see Section 4.3 for information on string processing facilities).

lns = readLines("datasets/lorem_ipsum.txt")
lns[1:2]

## [1] "Lorem ipsum dolor sit amet, consectetur adipiscing elit."       
## [2] "Donec lacus neque, rhoncus et ultricies volutpat, cursus in mi."

If you want to read all of the file as a single string, a solution is:

fileName = "datasets/lorem_ipsum.txt"; 
txt = readChar(fileName, file.info(fileName)$size)

5.1.4 Binary file input

Other functions that may be useful are readChar and readBin, but note that these are intended for binary-mode file connections.

5.2 Writing data to a file

5.2.1 The `write.table` function

The function write.table provides a simple interface for writing data to a file. It can be used to write a dataframe or a matrix to a file. For example, let’s load the iris dataframe:

data(iris)

and then write it to a text file:

write.table(iris, file="iris.txt",
                    col.names=TRUE, row.names=FALSE)

the above command will store it in the text file iris.txt with the labels for the variables it contains in the first row (col.names=T), but without the numbers associated with each row (row.names=F). The sep option is used to choose the separator for the data, the default is a blank space sep=" ", but you can choose a comma sep="," a semicolon sep=";" or other meaningful separators.

The write.table function can be used to write csv files.¹ For example, the following command will write the iris dataset to a CSV file:

write.table(iris, file="iris.csv", sep=",",
                    col.names=TRUE, row.names=FALSE)

5.2.2 Saving objecs in binary format

Probably the most convenent function to save R objects (dataframes, lists, matricies, etc…) in binary format is saveRDS:

saveRDS(iris, file="iris.rds")

the readRDS function can be used to read back the object into R:

iris_dset = readRDS("iris.rds")

5.2.3 Low-level file output

5.2.3.1 `cat`

A useful low-level function for writing to a file is cat. Suppose you have two vectors, one with the heights of 5 individuals, and one with an identifier for each, and you want to write these data to a file:

height = c(176, 180, 159, 156, 183)
id = c("s1", "s2", "s3", "s4", "s5")

you can use cat in a for loop to write the data to the file, but let’s first write a header

cat("id height \n", file="out_dir/cat_ex.txt", sep=" ", append=FALSE)

the first argument is the object to write, in this case a character string with the names of our variables to make a header, and a newline (\n') character to start a new line. Now thefor` loop:

for (i in 1:length(id)){
  cat(id[i], height[i], "\n", file="out_dir/cat_ex.txt",
      sep=" ", append=TRUE)}

note that this time we’ve set append=TRUE to avoid overwriting both the header, and any previous output from the preceding cycle in the for loop. We’ve been using a blank space as a separator, but we could have used something else, for example a comma (sep=",").

While using cat to automatically open and close a file as we did above is convenient, when we need to repeatedly write to the same file it’s more efficient to explicitly open a file connection first, write to it, and then close it as shown below:

fHandle = file("out_dir/test_write.txt", "w")

cat("id height \n", file=fHandle, sep=" ")
for (i in 1:length(id)){
    cat(id[i], height[i], "\n", file=fHandle,
        sep=" ")
}

close(fHandle)

5.2.3.2 `writeLines`

The writeLines function is the complement of the readLines function. In the next example we read-in a file with readLines, modify a line, and write the modified text with writeLines to another file:

lns = readLines("datasets/lorem_ipsum.txt")
lns[1] = "ipsum lorem"
writeLines(lns, "out_dir/writeLines_demo_1.txt")

The input to writeLines doesn’t need to be a character vector, a single string (even with multiple lines) will be fine too, as shown in the example below:

txt_lines = "Some text,
this is line two.
this is line three"
writeLines(txt_lines, "out_dir/writeLines_demo_2.txt")

5.2.3.3 Binary file output

Other useful functions include writeChar and writeBin, but note that these are intended for binary-mode file connections.

6 Graphics

There are four main plotting libraries that can be used in R. The first is the base graphics system that comes builtin with every R installation and will be described in this chapter. The other three main plotting libraries (ggplot2, lattice, and plotly), can be installed as additional packages. Each of these libraries provides a complete, independent system to generate plots in R.

Choosing one plotting library over the other is mostly a matter of personal preference because nearly any graphic that can be built with one library can also be built with the others. Some graphics are easier to build with one library than another and vice-versa. In recent years ggplot2 has gained lots of popularity and lattice is less popular than it used to be. Despite the increasing popularity of ggplot2 the base R graphics that are described in this chapter are still widely used. plotly is a recent entry and is somehow a special case because it is primarily designed to generate interactive graphics that can be displayed on html pages, while the other plotting libraries have very limited interactive functionality and are primarily designed to generate static high-quality graphics. plotly is also special because through the ggplotly function it can convert a ggplot2 graph into an interactive plotly graphic. Other graphics libraries that are worth mentioning, but will not be described in this guide are rgl, which allows the creation of interactive 3D graphics, and vegalite, another library designed for the creation of interactive html graphics.

Because the base R graphics library is still widely used and (in my opinion) is somewhat simpler to use for beginners, I would recommend learning it first. The ggplot2 library is described in Chapter 7, the plotly library is described in Chapter 8, and the lattice library is described in Chapter 9. Chapter 10 covers some plotting aspects (choosing colors, fonts, and using mathematical expressions in labels) that are common/similar across the different the different R plotting libraries. Chapter 11 gives tips and advice for preparing figures for academic journal publications, using any of the R graphics libraries. General advice (i.e. not tied to the use of any specific graphics system) on the construction of effective and professional graphics is given in Wilke (2019).

6.1 Overview of R base graphics functions

R base graphics has a number of “high-level” plotting functions. Some of these are listed in Table 6.1, and will be described in detail in the following sections. Graphics can also be produced using “low-level” plotting functions; these are introduced in Section 6.9.

Table 6.1: Some “high-level” plotting functions in the base R graphics system.
Function
`plot`
`barplot`
`boxplot`
`histogram`
`matplot`
`stripchart`
`interaction.plot`

6.2 The `plot` function

The plot function is most commonly used to draw a scatterplot of two variables, however if given a R object with a plot method as an argument, it will produce different types of graphics depending on the object it is plotting. Let’s look at an example of a scatterplot with some simulated data:

a = rnorm(5, 1.6, n=50)
b = rnorm(15, 4.3, n=50)

this creates two vectors of length 50 with values normally distributed, now we can plot the values of vector b, against the values of vector b with:

plot(x=a, y=b) ## or for short plot(a, b)

Figure 6.1: A scatterplot.

the resulting scatterplot appears in Figure 6.1.

If we were to plot the change of a variable over time it could be a good idea to connect the values at different time points in the plot with lines, this is easily achieved setting the option type. Below is an example, the result is shown in Figure 6.2.

ti = 1:50
b = rnorm(15, 4.3, n=50)
plot(ti, b, type="l")

Figure 6.2: Values connected by lines.

Some other possible values for the option type are p for points (the default), b for both points and lines, and o for overplotted points and lines (very similar to b).

6.3 Drawing functions

The plot function can be used for drawing mathematical functions, for example:

vec = seq(from=0, to=4*pi, length=120)
plot(vec, sin(vec), type="l")

Figure 6.3: Drawing a mathematical function.

in this case we use l for the plot type in order to obtain a continuous line rather than discrete points. It is also possible to plot markers at the points in which the function is actually evaluated. Using the option b for the plot type, both a continuous line and point markers are plotted. There are lots of options to define the appearance of a plot. Many of these options are presented in Section 6.5.

6.3.1 The `matplot` function

The matplot function can be used to plot the columns of a matrix against the columns of another once. The following example plots the sine and cosine functions together using the matplot function, the result is shown in Figure 6.4

a= seq(from=0, to= 2*pi, length=20)
s = sin(a)
c = cos(a)
aa = cbind(a, a) #matrix of hor coord
cs = cbind(c, s) #matrix of vert coord
matplot(x=aa, y=cs, type="l", lwd=1.8, ylab="sine and cosine functions")

Figure 6.4: Sine and cosine functions with matplot.

6.4 Common charts

6.4.1 Barplots

Barplots sometimes come in handy when you want to summarise your data. Suppose we have administered a test to three different groups of people, which we will designate as a, b and c. We want to summarise and compare the performance of each group with a nice graph, a barplot will make it. The data are stored in the file test.txt, in the format shown in Table 6.2.

Table 6.2: Data for the test example.
a	b	c
4	6	5
5	8	3
3	7	8
6	5	4
5	9	9
7	7	8
5	6	5
8	5	7
5	8	6
4	10	4

We can read in the file directly as a dataframe:

test = read.table("datasets/test.txt", header=TRUE)

We want to use the tapply function to get quickly summary tables with the means and standard deviations for the three groups. However the format of the data frame at this point is not suitable for the tapply function, because it has 3 observations for each row, and the tapply function can be used only with the format “one row per observation”, in which we have the values of the observations in one column and a set of “labels” identifying the group to which a given observation belongs to in another column. Fortunately, we can easily change the format of our dataframe with the stack command. What it does is just to create a single “values” vector from the three columns we had previously, and to add automatically another “index” vector with the labels we need:

test2 = stack(test)

we can have a look at the first elements of the new dataframe typing:

head(test2, n=10)

##    values ind
## 1       4   a
## 2       5   a
## 3       3   a
## 4       6   a
## 5       5   a
## 6       7   a
## 7       5   a
## 8       8   a
## 9       5   a
## 10      4   a

note that the stack function has automatically named the two vectors values and ind, we need to know these names to use the tapply function.

Now we’ll create the two summary tables using the tapply function, one with the means and one with the standard deviations for the three groups:

test_means = tapply(X=test2$values, IND=test2$ind, FUN=mean)
test_sd = tapply(X=test2$values, IND=test2$ind, FUN=sd)

Now we can draw a barplot displaying the means for each group:

barplot(test_means, col=c("darkred", "salmon2", "plum4"))

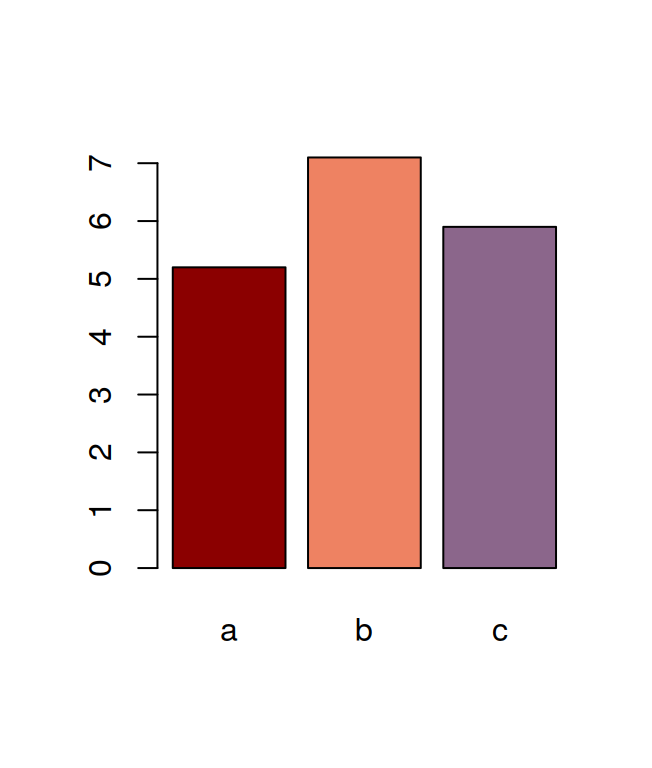
Figure 6.5: A barplot.

we’ve added colors to the graph using the col option. You can look at the resulting graph in Figure 6.5.

You can control the width of the bars specifying the width option, and setting the range for the x axis with the xlim option, specifying only the width does nothing, you must also set the xlim. You set xlim with a vector of the form xlim = c(from, to), in which from is the origin and to is the end of the axis. In the example below we will set xlim to go from 0 to 3 and the bars to have a width of 0.5:

barplot(test_means,col=c("darkred", "salmon2", "plum4"),
        xlim = C(0,3), width=0.5)

this sets the width of all bars at 0.5, we could specify the width for each single bar instead, by giving to width a vector with the width values for each bar.

You can also control the spacing between the bars with the space option. The default is set to 0.2.

6.4.1.1 Barplots with error bars

Now let’s say we want to get the same barplot but with error bars showing the standard deviation for each group. We could achieve this by adding lines to the current graph, but there is a better option: we can use the barplot2 function, which comes with the gplots library and provides an easy way of adding error bars to a barplot. So once we have the gplots package installed we first load it:

library(gplots)

and then we can draw our barplot with error bars. To get them, we need to set the option plot.ci=TRUE and then specify the upper and lower bounds of the error bars with the ci.u and ci.l commands. So we first create the values for ci.u and ci.l, so that the error bars represent one standard deviation around the mean. We’ll use the values from the two tables we had created before, with means and standard deviations for the three groups:

upper = test_means + (test_sd)
lower = test_means - (test_sd)

Now we can draw our barplot, you can see the result in Figure 6.6:

barplot2(test_means, col=c("darkred", "salmon2", "plum4"),
         plot.ci=TRUE, ci.u=upper, ci.l=lower)

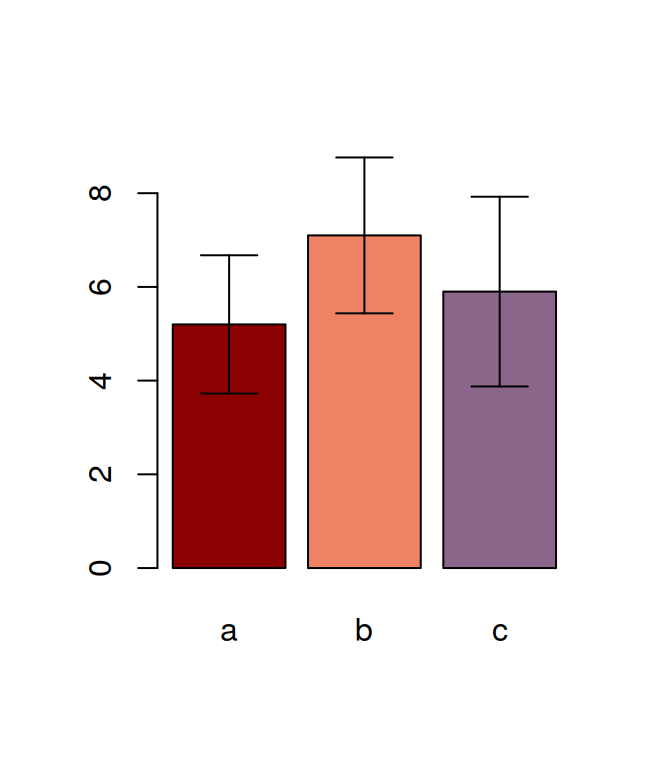
Figure 6.6: Barplot with error bars.

6.4.1.2 Barplots with stacked bars or with side-to-side bars

A barplot can be used to map the values of a variable across two factors. To illustrate this we’ll use the npk dataset, which contains data from a factorial experiment on the effects of N, P, K (nitrogen, phosphate, potassium) on the growth of peas.

data(npk)
npk$P = factor(npk$P, levels=c("0", "1"), labels=c("P=0", "P=1"))
npk$K = factor(npk$K, levels=c("0", "1"), labels=c("K=0", "K=1"))
head(npk)

##   block N   P   K yield
## 1     1 0 P=1 K=1  49.5
## 2     1 1 P=1 K=0  62.8
## 3     1 0 P=0 K=0  46.8
## 4     1 1 P=0 K=1  57.0
## 5     2 1 P=0 K=0  59.8
## 6     2 1 P=1 K=1  58.5

in the dataset N, P, and K are indicator variables for the application of the respective element (0=no, 1=yes). We renamed the levels of the P and K factors to make legends and strip labels easier to read. We first obtain means and standard deviations as a function of N and P with the tapply function:

mean_NP = tapply(npk$yield, list(npk$P, npk$N), mean)
sd_NP = tapply(npk$yield, list(npk$P, npk$N), sd)

in this case the resulting means and standard deviations are stored in a matrix instead of a vector. If we pass these values to the barplot2 function we obtain a stacked barplot (Figure 6.7):

barplot2(mean_NP, col=c("gray70", "indianred"),
         xlab="N", ylab="Mean yield")
legend(x=2, y=155, legend=c("P=0", "P=1"),
       fill=c("gray70", "indianred"), xpd=NA)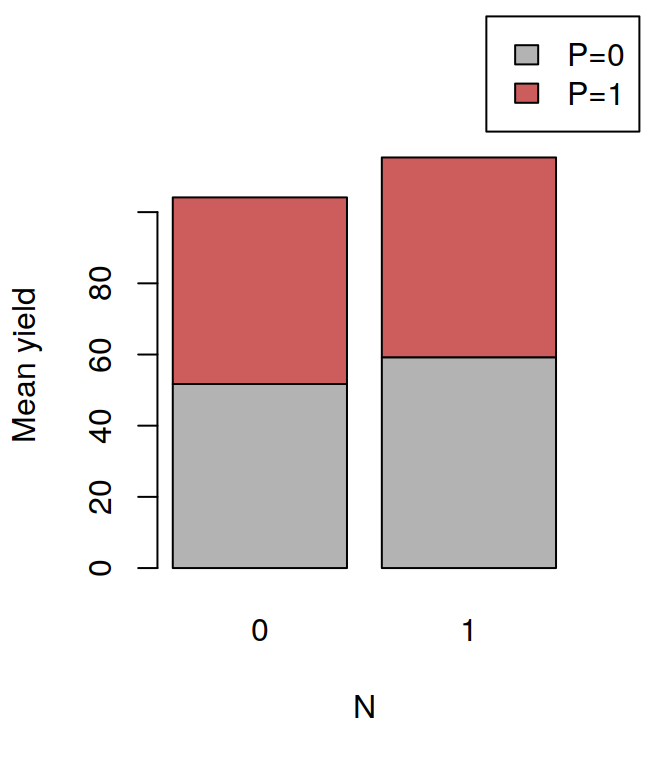

Figure 6.7: Stacked barplot.

we’ve added a legend manually; we could have passed the legend=T argument inside the barplot2 function to automatically add a legend instead, but the positioning of the automatic legend leaves often to be desired (see Section 6.6.1 more info on legends). The lower (gray) parts of the bars represent the mean yield without phosphate administration, while the upper (red) parts represent the mean yield with phosphate administration.

The same data can be displayed with a barplot with bars “side to side” (Figure 6.8). To obtain such a plot we need to set the beside argument to TRUE:

barplot2(mean_NP, plot.ci=T, ci.l=mean_NP-sd_NP, ci.u=mean_NP+sd_NP,
         col=c("gray70", "indianred"), legend=F, beside=T,
         xlab="N", ylab="Mean yield")
legend(x=5, y=85, legend=c("P=0", "P=1"),
       fill=c("gray70", "indianred"), xpd=NA)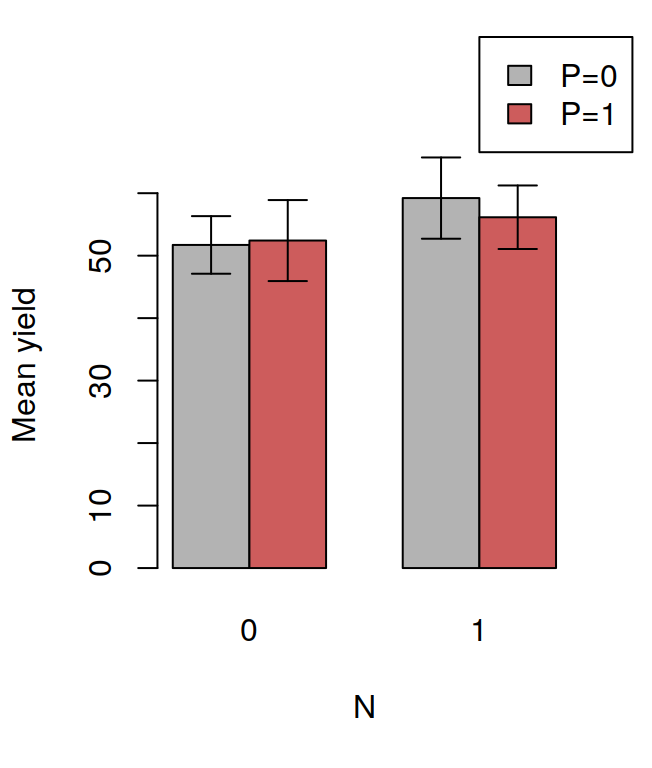

Figure 6.8: Barplot with bars side to side.

It would be somewhat difficult to add error bars to a stacked barplot, and the barplot2 function does not allow it (when beside is set to FALSE, settings plot.ci=TRUE is ignored). It is sensible, instead, to add error bars to the barplot with side to side bars, as we did in the last example.

6.4.2 Boxplots

Boxplots can be used to visualise the central tendency and the dispersion of the data for a given sample, and to directly compare these same characteristics for different samples. Let’s look at one of them, the data are organised in a dataframe in the file boxplot1.txt. They are the scores for two different groups (group a and group b) in a test. With the boxplot we want to see how the scores are distributed in the two groups. The dataframe contains a column score, with the score for each subject and another column group that defines the group a given observation comes from. So we first read in the dataframe, and then ask for the boxplots with the distribution of scores, as a function of the group they belong to.

dat = read.table("datasets/boxplot1.txt", header=TRUE)
boxplot(dat$score~dat$group, names=c("group a", "group b"))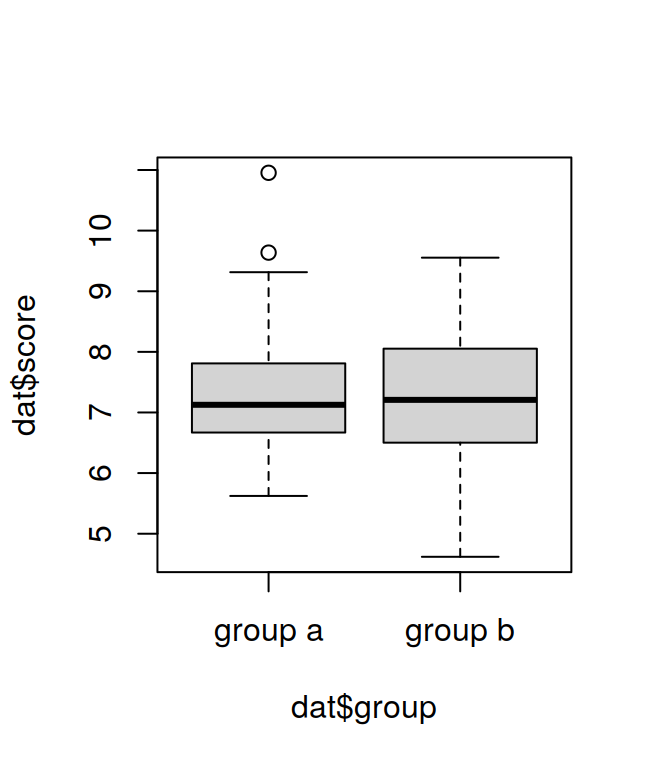

Figure 6.9: Boxplots comparing the distribution for two groups.

The results are in Figure 6.9, the thick black lines in the middle of the boxes represent the median, if this is about the middle of the box, it is consisten with the data having a normal distribution. The two lines that delimit the box are called “hinges”, and they are approximately the first and the third quartiles. The horizontal lines that form the `Ts’ above and below the box are called ``whiskers’’, and inside them are contained all the observations that fall within a distance of 1.5 times the size of the box, upwards or downwards. Points that fall outside this distance are outliers and they are represented as a circle. In our case there are two outliers in group a. Apart from checking if the distribution is normal, you can also check if the variances are approximately equal, by comparing the size of the boxes (the distance between the hinges). If one boxplot is clearly bigger than the other one (for example two times bigger), then the variances for the two groups are likely not to be equal.

6.4.3 Histograms

Histograms can be used to visualise the distribution of a sample, the function hist, can be used to plots a histogram of frequencies (counts) of the sample, or of its density function (setting the option freq=F). Let’s first create a sample with a normal distribution, and then plot its histogram, the result is in Figure 6.10.

my_distr = rnorm(100, 5, 1.7)
hist(my_distr)

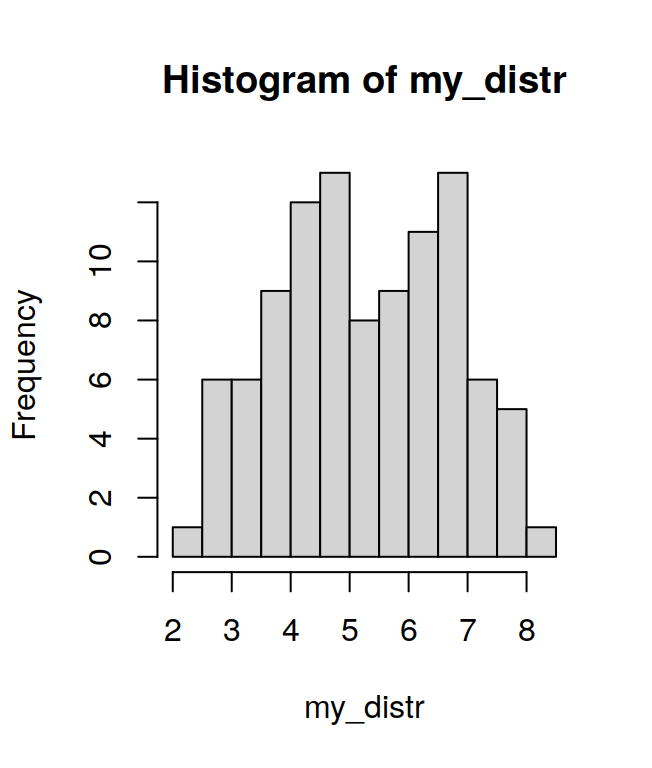
Figure 6.10: Frequency distribution of a random sample.

6.4.4 Stripcharts

If the groups contain a small number of observations, it might be better to use a stripchart to visualise their distributions. In a stripchart each point represents a single observation. By default they are drawn on a line, so if two observations have the same score, they overlap. To avoid this problem you can give a certain amount of jitter to the plot, so that observations with the same score are scattered a little and can be easily distinguished. Here’s the code for producing a stripchart, the data are in the file stripchart1.txt and they are arranged in the same way as the data in boxplot1.txt, just the sample sizes are smaller, with 6 observations per group.

stripchart(dat$score~dat$group, method="jitter",
           jitter=0.1, pch=1, vertical=TRUE)

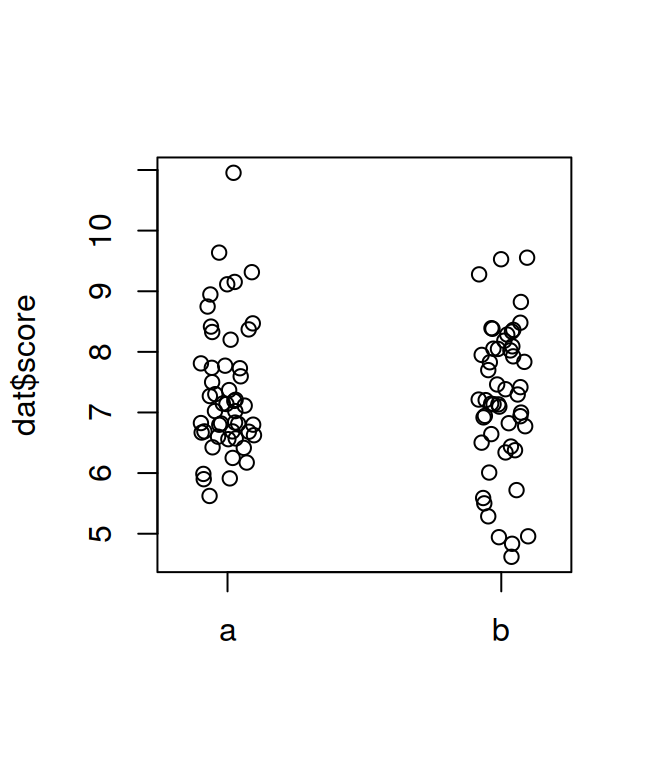
Figure 6.11: Stripchart example.

6.4.5 Interaction Plots

Interaction plots can be used to visualise the means for the levels of a factor, at the levels of another factor. In a two-way ANOVA design this type of plot would allow you to spot possible interactions between the two factors involved. To illustrate interaction plots we’ll use the built in R dataset ToothGrowth:

data(ToothGrowth) #load dataset
head(ToothGrowth)

##    len supp dose
## 1  4.2   VC  0.5
## 2 11.5   VC  0.5
## 3  7.3   VC  0.5
## 4  5.8   VC  0.5
## 5  6.4   VC  0.5
## 6 10.0   VC  0.5

that contains measurements of the length of odontoblasts (cells responsible for tooth growth) in 60 guinea pigs. Each guinea pig had received one of three doses of vitamin C (0.5, 1, and 2 mg/day) by one of two delivery methods, orange juice (OJ) or ascorbic acid (VC).

interaction.plot(x.factor=ToothGrowth$supp,
                 trace.factor=ToothGrowth$dose,
                 response=ToothGrowth$len,
                 ylab="Mean growth", xlab="Delivery",
                 trace.label="Dose")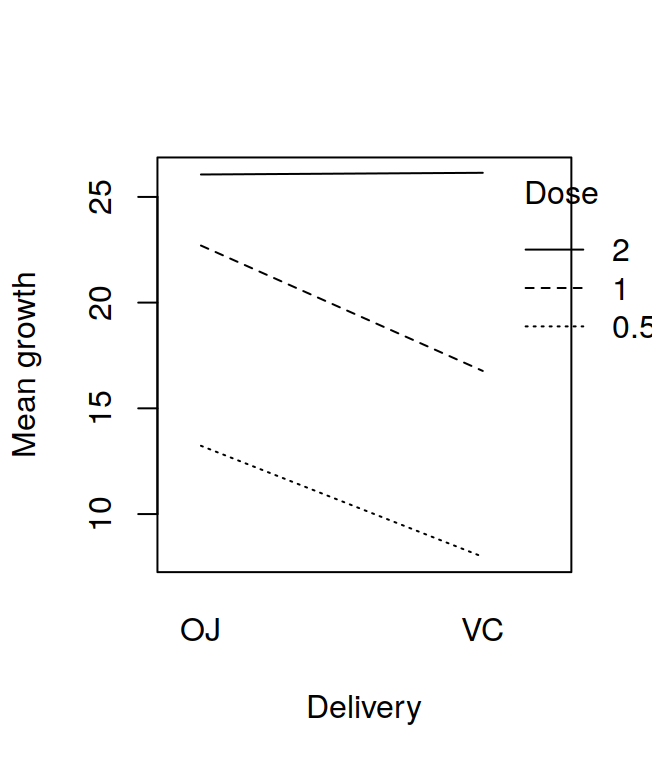

Figure 6.12: Interaction plot with different line types.

The first argument is the factor that will be represented on the x axis; the second argument is the trace factor, whose levels will be represented as lines of a different type, or of different colors. The third argument is the response variable. Note that we didn’t pass the mean of the response variable to the function, we passed the raw data and the function computed the mean for us. Optionally we can also set the x and y labels, as done in the example, and the trace.label, that sets the title of the legend. The plot is shown in Figure 6.12. It suggests the presence of an interaction because while at the lower doses OJ results in higher mean growth VC, at the highest dose the mean growth appears similar whichever delivery method is used.

The placement of the legend with interaction.plot is not always ideal. We can fix that by setting the legend argument to FALSE, and supplying a legend manually:

par(oma=c(0, 0, 0, 2.2))
interaction.plot(x.factor=ToothGrowth$supp,
                 trace.factor=ToothGrowth$dose,
                 response=ToothGrowth$len,
                 ylab="Mean growth", xlab="Delivery",
                 trace.label="Dose", legend=F)
legend(2.1, 27, legend=c("2", "1", "0.5"), lty=c(1,2,3),
       title="Dose", xpd=NA, bty="n")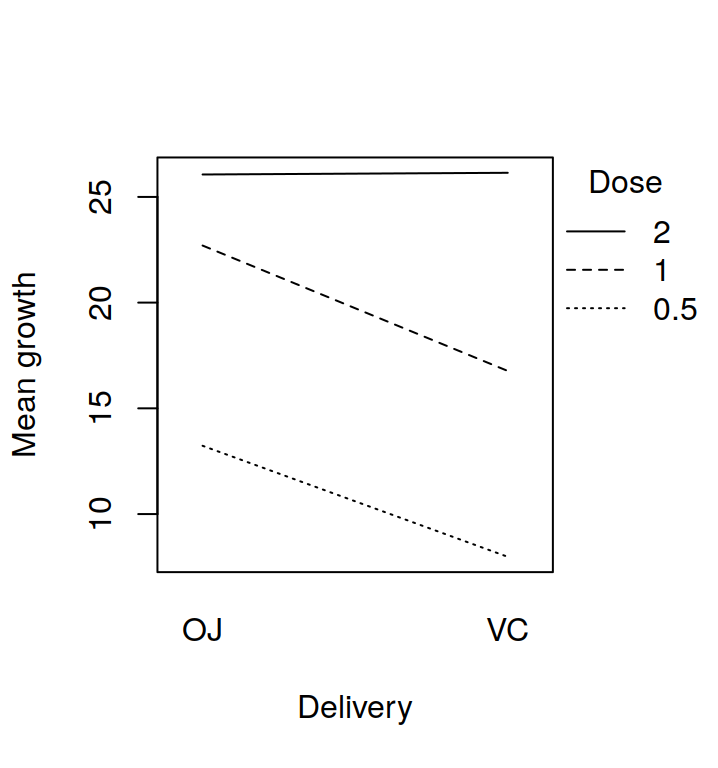

Figure 6.13: Interaction plot with manual legend.

Note how we also set the oma parameter to add an outer margin on the right side, so as to have enough space to place the legend outside the plot. We also set the xpd graphics parameter to NA so that the legend would not be clipped. Graphics parameters will be explained in Section 6.5.

Another good way to represent the levels for the trace factor, is through the use of symbols and/or colors, in the following graph (see the result in Figure 6.14) line type lty, symbols pch, and colors are used to differentiate between the levels of the trace factor. In order to get this you need to set the option type to b: that means use both line type and points (symbols); setting this option to l will give just different line types while setting it to p, will give just different symbols. In these examples I specified the line types and the symbols to use, but this is not necessary, if you don’t, R will cycle through different line types and/or symbols as needed to represent all the levels of the trace factor. See Section 6.5.2 for a description of the different line types, and Section 6.5.3 for a description of the different symbols available in R.

par(oma=c(0, 0, 0, 2.25))
interaction.plot(x.factor=ToothGrowth$supp,
                 trace.factor=ToothGrowth$dose,
                 response=ToothGrowth$len,
                 type="b", lty=c(3,2,1), pch=c(16,15,17),
                 col=c("gray60", "gray40", "gray10"),
                 ylab="Mean growth", xlab="Delivery",
                 trace.label="Dose", legend=F)
legend(2.2, 27, legend=c("2", "1", "0.5"), lty=c(1,2,3), pch=c(17,15,16),
       col=c("gray10", "gray40", "gray60"),
       title="Dose", xpd=NA, bty="n")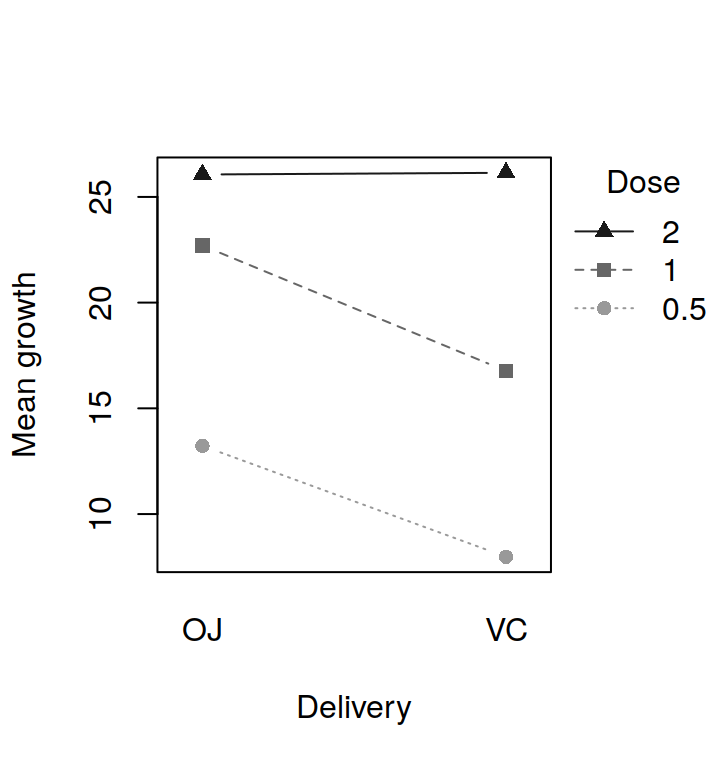

Figure 6.14: Interaction plot with different line types and different symbols.

6.4.6 Stem (lollipop) plots

There is no function in base R to generate a stem plot, also known as a “lollipop” plot. However, Matti Pastel published in his blog the following function to generate one:

stem = function(x, y, pch=16, linecol=1, clinecol=1, ...){
    if (missing(y)){
        y = x
        x = 1:length(x)
    }
    plot(x, y, pch=pch, ...)
    for (i in 1:length(x)){
        lines(c(x[i], x[i]), c(0,y[i]), col=linecol)
    }
    lines(c(x[1]-2,x[length(x)]+2), c(0,0), col=clinecol)
}

Figure 6.15 shows a stem plot generated with this function using the code below:

x = seq(0, 2*pi, 0.25)
y = sin(x)
stem(x, y, xlab="x", ylab="sin(x)")

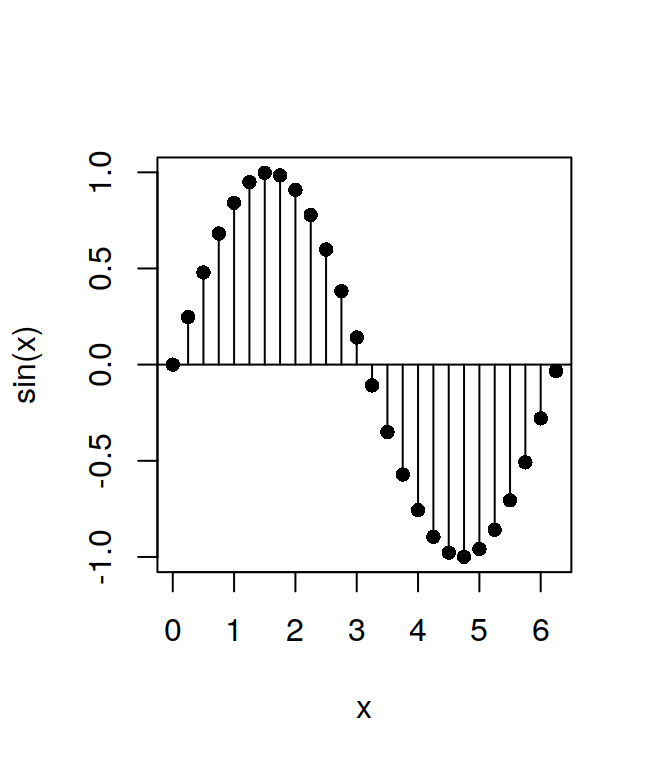
Figure 6.15: Stem plot.

6.5 Setting graphics parameters

Graphics parameters allow you to tweak many elements of a plot, such as the font for the labels, the symbols or line types to use and so on, see ?par to get a full list and description of these parameters. Graphics parameters can be set and accessed with the function par, called without arguments, as par(), it will give you a full list of the current defaults, if you want to query only one or a few parameters use:

par("lwd")          ## see current line width

## [1] 1

par(c("lwd","pch")) ## see lwd and plotting symbols

## $lwd
## [1] 1
## 
## $pch
## [1] 1

to change the value of a parameter you can use:

par(lwd=1.4)       ## change line width
par(pch="*",       ## change plotting symbol
    bg ="gray80")  ## use a light gray background

Moreover, most plotting functions like plot, and barplot, allow you to set some of the parameters for the current plot as an argument to the function itself, for example in plot you can choose the type of plot (points vs lines) and the plotting symbol as options with type and pch:

d = rnorm(15,4,2)
e = rnorm(15,9,3)
plot(d~e, type="p", pch=3)

The following sections will give a more in depth explanation of some graphics parameters. Before that, however, we’ll have a closer look at how to use par.

6.5.1 Saving and restoring graphics parameters

Often you’ll want to change the graphics parameters only for a few plots, and then reset them back to the defaults. The function par when used to change the value of some graphics parameters returns a list with the old values of the graphics parameters that have changed:

par("lwd", "col") #these are the default parameters

## $lwd
## [1] 1
## 
## $col
## [1] "black"

oldpar = par(lwd=2, col="red") #while changing the parameters
                                #we store the old values in a list
oldpar

## $lwd
## [1] 1
## 
## $col
## [1] "black"

s = seq(0, 10, .1) 
plot(s, sin(s))           #we plot something

par(oldpar)              # and then we restore the old parameters

note that calling par, opens a graphics device if one is not already open, the changes you do using par apply only to this graphics device, any other new graphic device that you open will have the default graphics parameters.

6.5.2 Line type with the `lty` parameter

There are six line types that you can call in R just with names or numbers (actually there are seven, the first one is “blank” or 0 which just draws nothing). These are listed in Table 6.3 and shown in Figure 6.16. There is a different, more complicated way for setting many more line types, please, consult the manual for further information on that.

Table 6.3: The six default line types in R.
No.	Name
1	solid
2	dashed
3	dotted
4	dotdash
5	longdash
6	twodash

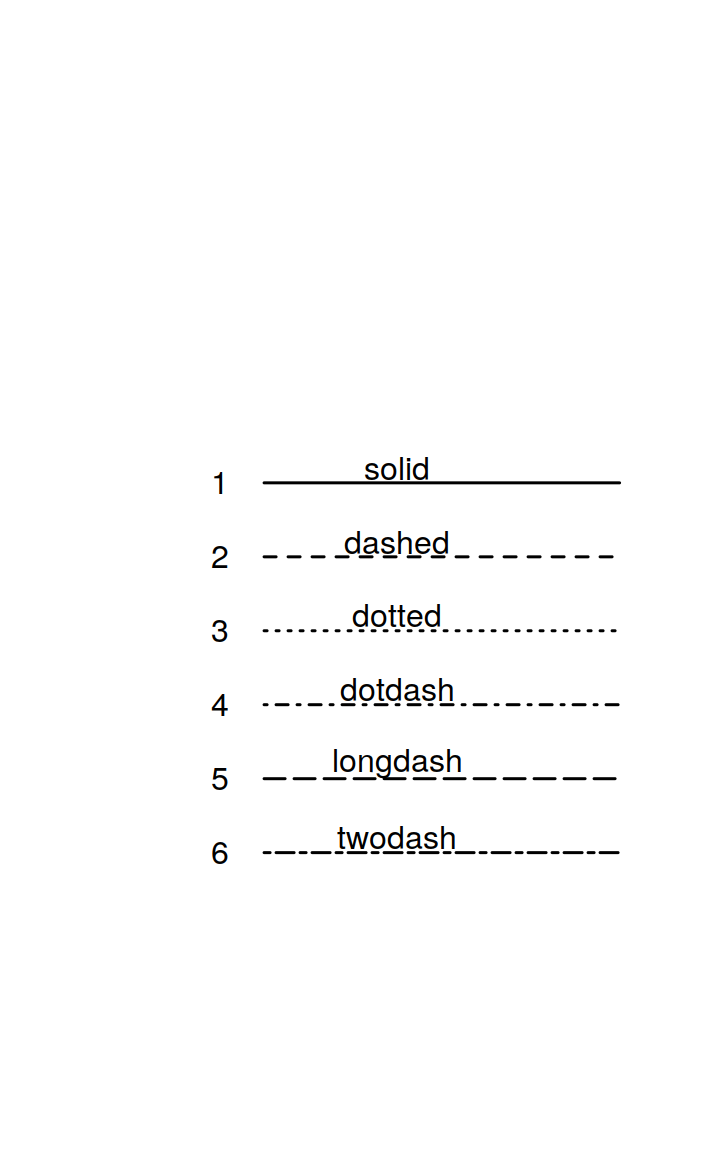
Figure 6.16: The six default line types in R

6.5.3 Symbols with the `pch` parameter

pch is a graphical parameter for changing the way points are plotted in certain graphical functions. This parameter can be set in two ways, the first one is to give a symbol to be plotted as a character, for example

pch="+"
pch="T"
pch="*"
pch="3"

in this case you enclose the character you want to use between quotes, you can’t use more than a single character. The other way to set the pch is to use a number between 0 and 25, which will select one of 26 special symbols available for plotting (see Figure 6.17), like circles, triangles, and so on:

pch=1
pch=3
pch=5

Figure 6.17: Plotting symbols from 0 to 25

6.5.4 Fonts

The par interface can be used to set a number of font parameters. One thing to keep in mind is that certain font properties can also be set at the device (X11, pdf, png, etc…) level. Properties set with par after opening the device will override properties set at the device level. Additionally, each device deals with fonts differently, and setting a given font family with par for a given deice (e.g. X11) will not necessarily work for other devices (e.g. pdf). The font parameters that can be set through the par interface are listed in Table 6.4

Table 6.4: Parameters for fonts.
Parameter	Function
`family`	font family (e.g. “sans”, “serif”, “mono”)
`font`	font type for text (1=plain, 2=bold, 3=italic, 4=bold italic)
`font.axis`	font type for axis annotation (1=plain, 2=bold, 3=italic, 4=bolditalic)
`font.lab`	font type for x and y labels (1=plain, 2=bold, 3=italic, 4=bolditalic)
`font.main`	font type for main titles (1=plain, 2=bold, 3=italic, 4=bolditalic)
`font.sub`	font type for sub titles (1=plain, 2=bold, 3=italic, 4=bolditalic)
`ps`	point size of text

The various parameters starting with “font” (font, font.axis, font.lab, etc…) do not change the family, they change the style (e.g. plain, bold, italic). These parameters are set via a number; a value of 1 corresponds to a normal (or plain) style, 2 to bold, 3 to italics, 4 to bold italics, and 5 will map the font to a symbol, an usage example is show below (the resulting plot is shown in Figure 6.18):

x = seq(0, 2*pi, 0.1)
y = sin(x)
par(font=3)
plot(x, y, xlab="x-axis label", ylab="y-axis label", main="Sin(x)", type="b")
text(1.5, -0.5, "Some text \nin italics")

Figure 6.18: Changing font style.

Note that setting font only changes the font style of plotted text. If you want to change the font style of other textual elements such as the axis labels or the plot title you have to set the corresponding graphics parameters, as shown in the example below (the resulting plot is shown in Figure 6.19):

par(font=3, font.axis=3, font.lab=3, font.main=4, font.sub=2)
plot(x, y, xlab="x-axis label", ylab="y-axis label",
     main="Sin(x)", sub="subtitle", type="b")
text(1.5, -0.5, "Some text \nin italics")

Figure 6.19: Changing font style for other textual elements.

The ps parameters sets the base point size of the font; the final pointsize is scaled by the cex parameter (i.e. text size = ps*cex), so if cex is different than 1, the final pointsize will not be equal to ps. Note that ps changes only the size of the text font:

x = seq(0, 2*pi, 0.1)
y = sin(x)
pdf(file="test_plot.pdf", pointsize=12)
plot(x, y, xlab="x-axis label", ylab="y-axis label", main="Sin(x)", type="b")
dev.off()

while setting the pointsize when opening certain graphics devices, such as the pdf device, changes the size of both the font and the plotting symbols:

x = seq(0, 2*pi, 0.1)
y = sin(x)
pdf(file="test_plot.pdf", pointsize=24)
plot(x, y, xlab="x-axis label", ylab="y-axis label", main="Sin(x)", type="b")
dev.off()

The documentation for the graphics parameter ps also says that “unlike the pointsize argument of most devices, this does not change the relationship between mar and mai (nor oma and omi).”. I’m not sure what this means, but just be aware setting ps with a call to par or setting pointsize when opening a graphics device are not equivalent. Also, keep in mind that if you set the font size when you open a graphics device, the setting may be overridden by subsequent calls to par:

pdf(file="test_plot.pdf", pointsize=12) #set font and symbol size in `pdf` call
par(ps=24) #override the `pointsize` setting for font
           #(but not plotting symbols)
plot(x, y, xlab="x-axis label", ylab="y-axis label", main="Sin(x)", type="b")
dev.off()

cex also overrides the graphics device settings:

pdf(file="test_plot.pdf", pointsize=24) #set font and symbol size
                                        #in `pdf` call to 24
par(cex=0.5) #scale the `pointsize` by half, so now it is 12
plot(x, y, xlab="x-axis label", ylab="y-axis label", main="Sin(x)", type="b")
dev.off()

The par setting family can be used to choose a serif, sans, or mono font. The following example shows how to make a plot (displayed in Figure 6.20), with a mono family font:

par(family="mono")
plot(1:10, main="Mono font")

Figure 6.20: Changing font family.

Note that serif, sans, or mono are generic font families. The actual font family (e.g. Helvetica, Arial, Times New Roman, etc…) that gets used depends on a mapping, which is different between graphics devices, between these generic names and an actual system font. It is possible to directly specify a system font when calling par. Figure 6.21 shows a plot with the Palatino font set through par:

plot.new(); plot.window(xlim=c(1,10), ylim=c(1, 10))
par(family="Palatino")
plot(1:10)

Figure 6.21: Plot with Palatino font.

however, this may or may not work depending on 1) whether the font is actually installed on your system 2) the graphics device (not all graphics devices have access to all installed system fonts). More information on how to use system fonts is available in Chapter 10.3.

Not all graphics devices have access to all installed system fonts. For workarounds see Chapter (???)(fonts).

6.5.5 Colors

Table 6.5 lists a number of color parameters that can be set through the par interface. See Section 10.1 for indications on how to speficy colors in R.

Table 6.5: Color parameters that can be set through the `par` interface.
Parameter	Function
`col`	plotting color
`col.axis`	color for axis annotation
`col.lab`	color for x and y labels
`col.main`	color for main title
`col.sub`	color for sub-titles
`bg`	background color
`fg`	foreground color

6.6 Adding elements to a plot

6.6.1 Adding a legend

Some plotting functions (e.g. interaction.plot) by default add a legend to the graph, or allow you to add a legend by setting an option inside the function (e.g. barplot). However, the default settings for the legend, such as positioning, text or symbols, might not be suitable for your graph, in which case you need to turn off the default legend, and add a customised legend with the legend function. You may also need the legend function if the plotting function that you’re using does not automatically add a legend, or if you’re plotting from scratch. Figure 6.22 shows a plot with a legend for the different plotting symbols:

data(iris)
d_set = iris[iris$Species=="setosa",]
d_ver = iris[iris$Species=="versicolor",]
d_vir = iris[iris$Species=="virginica",]
ylim = c(min(iris$Sepal.Length), max(iris$Sepal.Length))
xlim = c(min(iris$Petal.Length), max(iris$Petal.Length))
plot(d_set$Petal.Length, d_set$Sepal.Length, xlim=xlim, ylim=ylim, pch=15,
     xlab="Petal Length", ylab="Sepal Length")
points(d_ver$Petal.Length, d_ver$Sepal.Length, pch=16)
points(d_vir$Petal.Length, d_vir$Sepal.Length, pch=17)
legend("topleft", legend=c("Setosa", "Versicolor", "Virginica"),
       pch=c(15, 16, 17))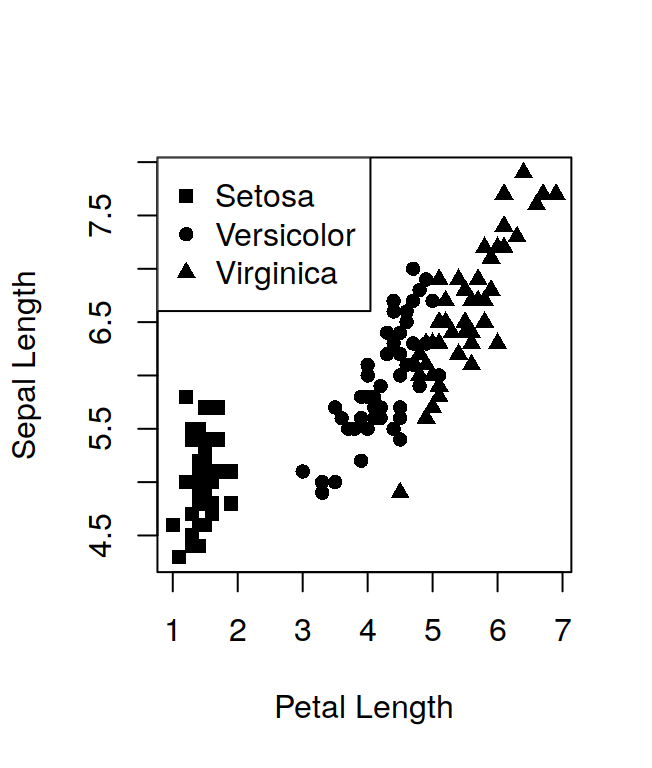

Figure 6.22: Plot with legend for plotting symbols.

The last two lines of code add the legend. The first argument given to the legend function, topright, indicates the position where we want the legend to appear, other possible values are bottomright, bottomleft, right, bottom, center and so on. It is also possible to specify the position of the legend by giving the coordinates of its top-left corner, for the above example we might have written:

legend(x=2.5, y=7, legend=c("Setosa", "Versicolor", "Virginica"),
       pch=c(15, 16, 17))

The text of the legend is passed as a character vector, each element of the vector represents one item of the legend. The next argument, pch indicates that we want each element to represent different plotting symbols, and specifies the plotting symbols to use (15, 16, and 17).

If you do not want a box around the legend, you can set the bty argument to n (default setting is o, which adds the box). If you choose to enclose the legend into a box, you can set its background color through the bg argument.

Sometimes we can encode groupings by more than one dimension. Figure 6.23 shows the data plotted previously with iris species differentiated by both plotting symbols and colors:

library(RColorBrewer)
pal = brewer.pal(3, "Pastel1")
plot(d_set$Petal.Length, d_set$Sepal.Length, xlim=xlim, ylim=ylim, pch=15,
     xlab="Petal Length", ylab="Sepal Length", col=pal[1])
points(d_ver$Petal.Length, d_ver$Sepal.Length, pch=16, col=pal[2])
points(d_vir$Petal.Length, d_vir$Sepal.Length, pch=17, col=pal[3])
legend("topleft", legend=c("Setosa", "Versicolor", "Virginica"),
       pch=c(15, 16, 17), col=pal)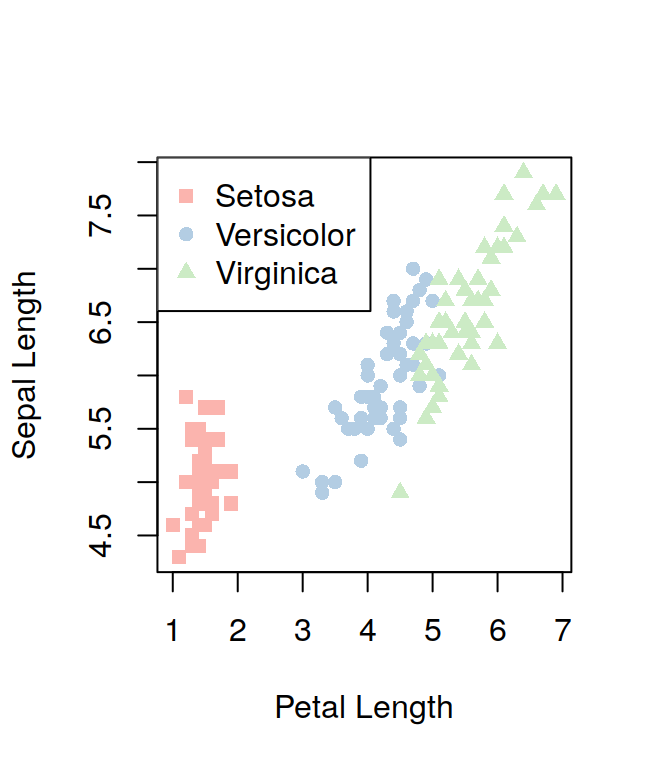

Figure 6.23: Plot with legend for plotting symbols and colors.

the only difference with the previous legend is that now we pass an additional argument, col to indicate that we want each element to represent different colors, and specifies the colors to use (those in the pal vector).

We’ve already seen an example of a complex legend specifying different plotting symbols, line types, and colors for its elements in Section 6.4.5.

Figure 6.24 shows an example of a legend for a barplot. In this case the legend was positioned outside the plot. Note how we set the xpd argument to NA to avoid the legend being clipped inside the plotting area. Depending on the size and placement of the legend we may also need to enlarge either the margings (mar) or the outer margins (oma) to leave enough room for the legend. An example where this was needed was given in Section 6.4.5; for an overwiew of plotting regions and margins see Section 6.8. Finally, note how we set the ncol argument to indicate that the legend should have 4 columns:

data(HairEyeColor)
par(mfrow=c(1,2))
barplot2(HairEyeColor[,,"Male"], beside=T, xlab="Eye color", ylab="# cases",
         col=c("black", "brown", "red", "gold"), ylim=c(0, 72), las=3)
title(main="Males", line=-1)
box()
legend(8, 90, legend=c("Black", "Brown", "Red", "Blond"),
       fill=c("black", "brown", "red", "gold"),
       title="Hair color", ncol=4, xpd=NA, bty="n")

barplot2(HairEyeColor[,,"Female"], beside=T, xlab="Eye color", ylab="# cases",
         col=c("black", "brown", "red", "gold"), ylim=c(0, 72), las=3)
title(main="Females", line=-1)

box()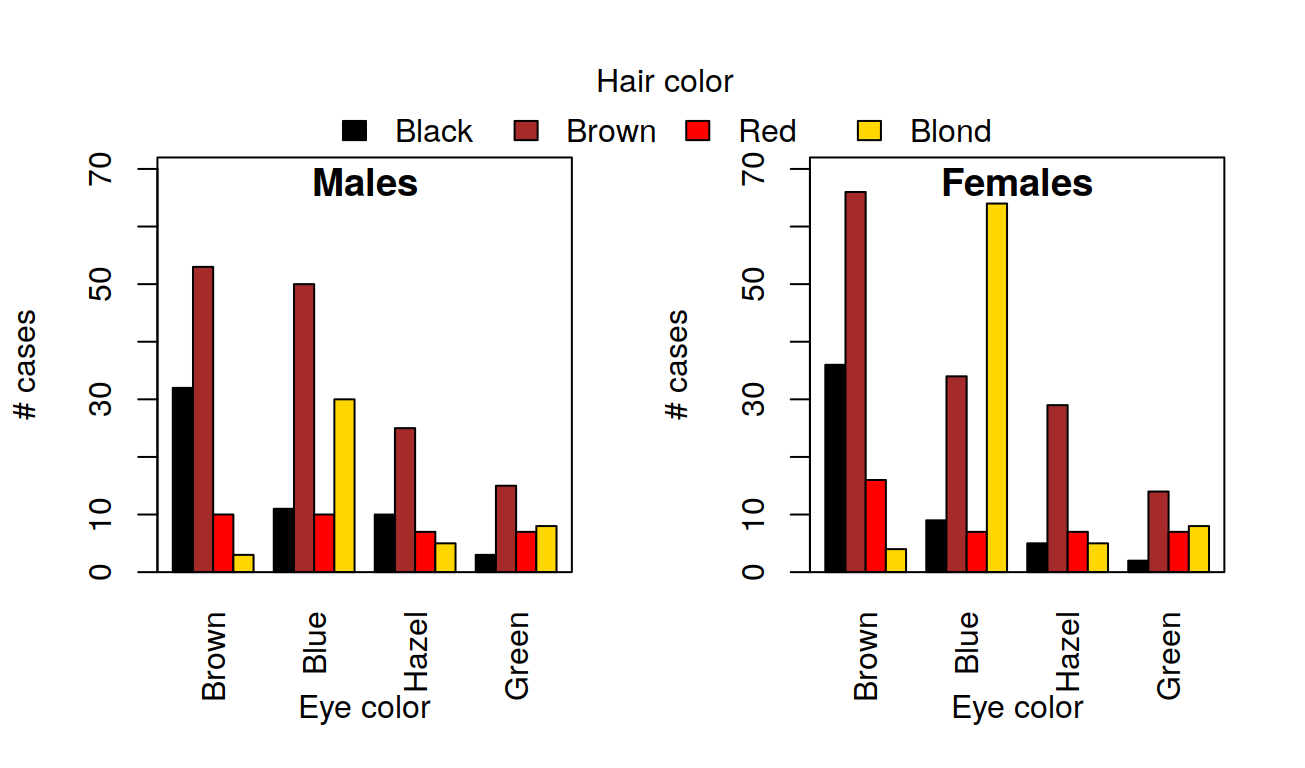

Figure 6.24: Barplot with a legend outside the plot.

6.6.2 Adding text

You can insert text in a graph with the text function, you have just to specify the x and y coordinates of the point on which to center the text:

plot(x, y)
text(x=3, y=1.5, "mean for control group")

if you want to use mathematical symbols you can use the expression function:

text(x=3, y=1.5, expression(alpha))

more details on how to use mathematical symbols are given in Section 10.2 .

6.6.3 Adding a grid

A grid can be easily added to an existing plot with the function grid

s = seq(from=0, to=2*pi, length=100)
plot(s, sin(s))
plot(s, sin(s), type="l")
grid() ##add the grid

The default color for the grid is lightgray, you can choose another color setting the col option:

grid(col="red")

6.6.4 Setting the axes

If you don’t like the way the axes are set for a given plot, you can draw the plot without them first, and then add customised axes with the `axis+ function. There are several ways to get rid of the default axes on a plot:

plot(1:10, axes=FALSE) #do not draw any axes or box around
                       # the plot
plot(1:10, xaxt="n")   #don't draw the x axis 
plot(1:10, yaxt="n")   #don't draw the y axis

Once you’ve removed of one or more axes you can draw them calling the axis function:

axis(1, at=seq(1, 10, 3), labels=as.character(seq(1, 10, 3)))

the first argument specifies the side on which the axis should be drawn, 1 means the bottom axis, 2 the left axis, 3 the top axis, and 4 the right axis. See ?axis for other arguments to the function.

6.7 Creating layouts for multiple graphs

6.7.1 `mfrow` and `mfcol`

The parameters mfrow and mfcol allow you to divide the graphics device you’re using (e.g. X11 or pdf) into multiple boxes, each box will contain a new figure. These parameters are set giving a vector of the form:

par(mfrow=c(n_rows, n_columns))

where n_rows is the number of rows and n_columns is the number of columns you want for your layout. For example, the following will create a layout with 2 rows and 3 columns as you can see in Figure 6.25:

par(mfrow=c(2,3))
symb = as.character(1:6)
for(i in 1:6){
    plot(1, 1, pch=symb[i], xlab="", ylab="")
}

Figure 6.25: A 2x3 Layout with mfrow

mfcol works exactly the same way as mfrow, but the figures are drawn in sequence by column rather than by row, for example the following code yields Figure 6.26

par(mfcol=c(2, 3))
symb<-as.character(1:6)
for(i in 1:6){
  plot(1, 1, pch=symb[i], xlab='', ylab='')
}

Figure 6.26: A 2x3 Layout with mfcol

of course you can get other layouts, try:

par(mfrow=c(2,2)) ## 4 boxes
par(mfrow=c(1,3)) ## one row, 3 cols

Rather than having the figures drawn sequentially, following the order determined by mfrow or mfcol, it is possible to specify directly the position for the next figure using the mfg parameter. The next example will draw the plot in the slot defined by the crossing between the second row and the first column of a 2x2 layout:

par(mfrow=c(2,2)) ##create 2x2 layout
par(mfg=c(2,1))   ##set next fig at 2dn row, 1st col
plot(1:100, sin(1:100))

6.7.2 `layout`

A more flexible way to divide a graphics device into multiple plotting regions is given by the layout function. With the layout function, the graphics device is divided into a matrix of n_rows x n_cols sub-regions, and each figure is assigned to one or more of these sub-regions. Let’s look at an example:

m = matrix(c(1,2,3,4), nrow=2, byrow=TRUE)
m

##      [,1] [,2]
## [1,]    1    2
## [2,]    3    4

layout(m)

the matrix m we’ve created, completely defines our layout for the graphics window. The window is divided into 2 x 2=4 sub-regions. Moreover, the first figure is assigned the sub-region on the top-left of the window, the second figure the sub-region at the top-right, the third the region at the bottom-left, and the fourth the region at the bottom-right. This example is in itself not very different from what we would get with mfrow, however two key differences make layout more powerful than mfrow. First, it is possible to assign more than a single sub-region to a figure, for example:

m = matrix(c(1,1,2,3), nrow=2, byrow=TRUE)
m

##      [,1] [,2]
## [1,]    1    1
## [2,]    2    3

layout(m)

divides the graphics window into 4 sub-regions as above, but the first figure is assigned the two sub-regions on top, while the bottom-left sub-region is assigned to the second figure, and the bottom-right to the third.

The second key difference with mfrow is that with layout it is possible to define the width of the columns, and the height of the rows composing the array of sub-regions in the graphics window. Width and height are given as vectors of relative widths and heights. For example:

m = matrix(c(1,1,2,3), nrow=2, byrow=TRUE)
m

##      [,1] [,2]
## [1,]    1    1
## [2,]    2    3

layout(m, width=c(1/4,3/4), height=c(2/3,1/3))

will make the first column 1/4 of the total width, and the second column the other 3/4, the same reasoning applies to the row heights. The command layout.show(n), where n is the number of $n^{th}$ figure that is going to be plotted, will show the outline of its layout in the graphics window.

6.8 Graphics device regions and coordinates

In traditional R graphics the graphics device (e.g. the X11 window where your plot and annotations appear) is divided into different regions (see Figure 6.27):

the plotting region is the area in which the drawing of points or lines representing your data occur. The plotting region is contained into the figure region
the figure region is composed of the plotting regions plus the margins where the plot can be annotated with labels for the axes, a title etc…
the outer margins surround the figure region. The outer margins are usually set to zero (i.e. there are no outer margins), they become useful, however, for annotating multiple plots that appear on the same page (e.g.~plots generated with `mfrow+). When multiple plots are arranged on the same page (or device), each is assigned a figure region with its own margins, so the outer margins can be used for annotating the overall page (see Figure 6.28).

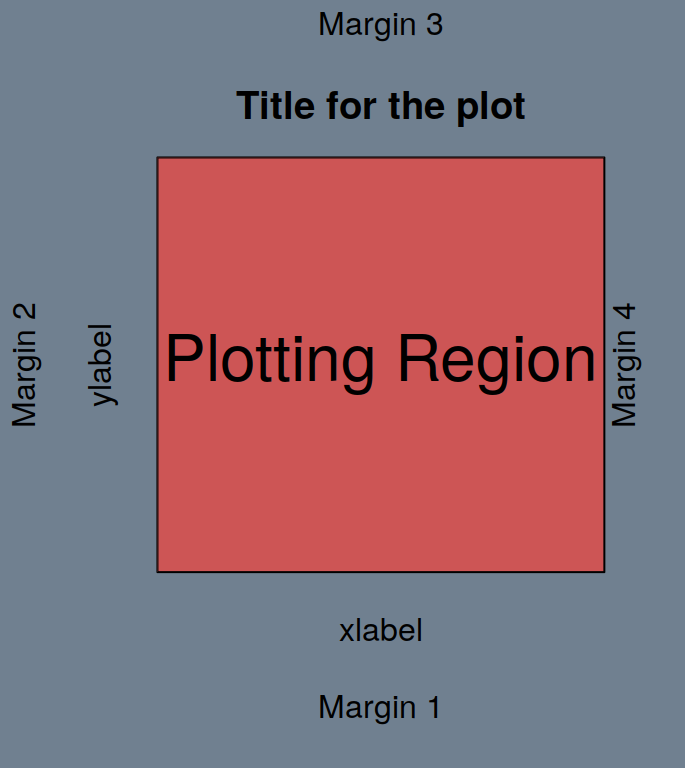
Figure 6.27: The figure region includes the plotting region and the margins.

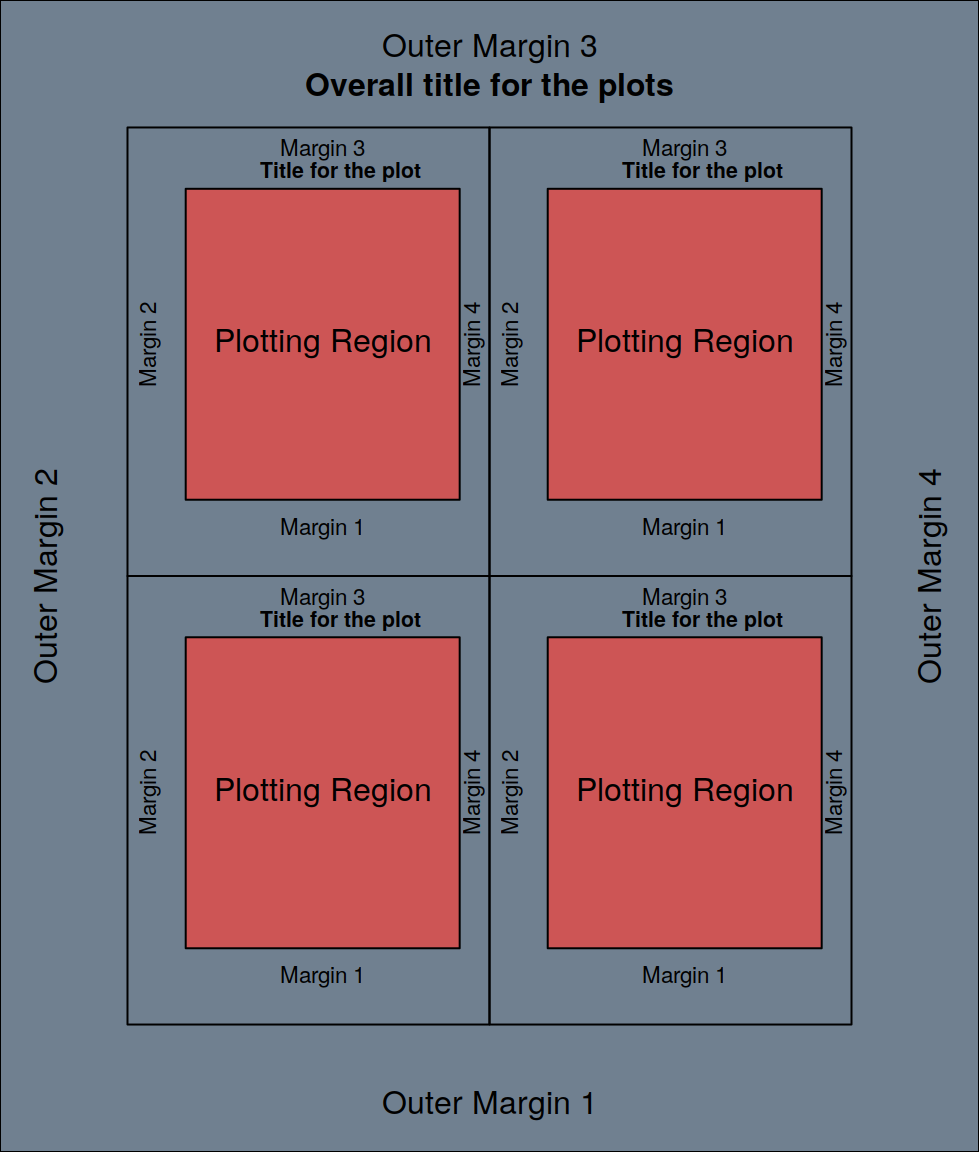
Figure 6.28: Device with outer margins and multiple figure regions.

The width and height of the device is usually specified when the device is opened, for example:

X11(width=8, height=8)

opens a X11 device measuring 8x8 inches. The size of an open device can be queried with par("din"), this is a read only graphics parameter, which I guess means that once a certain device is opened its size cannot be changed (an X11 window however can be re-sized with the mouse, and par("din") correctly reports the new size). Different units of measure can be used to specify the size of the areas inside a device, some of these units will be shortly introduced here, others will be explained when they are first used:

inches: an inch is 2.54 centimetres (notice that the actual physical measure of what you see on your monitor may depend on your monitor’s settings, e.g. dpi, screen resolution, etc…)
lines of text: this measure depends on the value of cex and pointsize
Normalised Device Coordinates (NDC): the device region is 1x1 NDC whatever the actual physical measure. The lower left corner has coordinates (x=0, y=0) and the upper right corner (x=1, y=1). Using NDC thus the size of regions inside the device can be specified in relative terms to the device size.

In the next paragraphs the graphics parameters for controlling the different regions inside the device will be explained. Always keep in mind the layout of a graphics device in R (see Figure 6.27 and Figure 6.28).

6.8.0.1 Figure region

The figure region can be set either in inches or in normalised device coordinates.

fig: NDC coordinates of the device in the form c(x1, x2, y1, y2), where (x1, y1) are the coordinates of the lower left corner, and (x2, y2) are the coordinates of the upper right corner). Example:

par(fig=c(0.1, 0.5, 0.1, 0.6)) 
plot(1:10)
par(fig=c(0.5, 1, 0.1, 0.6)) # the next call to plot will erase the
                             # current plot
plot(1:10)
par(fig=c(0, 0.5, 0.1, 0.6), new=TRUE) # the next call to plot will not 
                                       # erase the current plot
plot(1:10)

as shown in the example to change the figure region without starting a new plot add new=TRUE, this may be used for creating complex arrangements for multiple plots within the same device.

fin: the figure region dimension (width, height) in inches. Example:

par(fin=c(5,5))

6.8.0.2 Plotting region

plt: a vector of the form c(x1, x2, y1, y2) giving the coordinates of the plot region as fractions of the current figure region
pin: the current plot dimensions, (width,height), in inches

6.8.0.3 Margins

mar: the width of the margins for the four sides of the plot, specified in terms of lines of text. The margins are specified in the form c(bottom, left, top, right). The default is c(5,4,4,2) + 0.1. Example:

par("mar") # get current margins size
par(mar=c(6, 2, 3, 0) + 0.1) #set new margins size

mai: the same as mar, but the unit of measure is inches rather than lines of text

6.8.0.4 Outer margins

oma: a vector of the form c(bottom, left, top, right) giving the size of the outer margins in lines of text
A vector of the form c(bottom, left, top, right) giving the size of the outer margins in inches
A vector of the form c(x1, x2, y1, y2) giving the outer margin region in normalised device coordinates (NDC)

6.9 Plotting from scratch

The high-level plotting functions such as plot, histogram, barplot and so on, provide a good and quick way to produce graphs. Plotting from scratch, using the low-level plotting commands is generally not necessary, unless you want to create some new, customised plotting functions. Learning to plot “from scratch”, however is a very good way to learn how graphics parameters work, which is often necessary to customise plots created with the high-level plotting functions.

We’ll start with a very simple example of a scatterplot:

plot.new()
plot.window(xlim=c(0,10), ylim=c(0,10))

the plot.new() command creates a frame for plotting, and opens a graphics device if one is not already opened. plot.window defines the limits for the x and y axes, points outside these limits will not appear in the plot. After these two commands we’re ready to do the actual drawing:

points(x=c(1,2,3,4,5,9), y=c(2,5,3,4,5,3))
axis(side=1)
axis(side=2)

points will draw points at the coordinates given in the x an y arguments. To complete this very minimal plot you need at least some axes. The axis function adds the axis, the side argument specifies where the axis should be drawn, 1 means at the “bottom”, 2 at the “left” side, and so on in a clockwise fashion.

6.10 Managing graphic devices

6.10.1 Opening another graphics window

When you issue the command for a graph R opens a window to show it, if you afterwards issue another command for a graph, if the previous window is still open, R doesn’t open another one, but rather replaces the old graph with the new one. If you wish to show the new graph in a separate window, you have to open the graphic device yourself, this is accomplished with the command X11 under Unix and with the command windows under the Windows OS. The device window can also be closed from the command line with:

dev.off()

if you have many device windows open and you want to close them all at once use:

graphics.off()

For further functions to manage multiple device windows see ?dev.set.

6.10.2 Exporting graphics

With R it’s also possible to export your graphics in different file formats, such as JPEG or postscript files. To do this, you need to open first the graphics device you want to use, then insert the command for the graphic, and finally turn off the graphic device. Here’s an example of how to produce a graphic in JPEG format:

jpeg(file="plot.jpeg")
plot(x,y)
dev.off()

Other devices you can use, with their corresponding file format are pdf, postscript, png and bitmap.

7 ggplot2

ggplot2 is an add-on R library for generating plots. It differs radically from traditional plotting libraries, such as the base R graphics library, because it is based on a formal high-level model of statistical graphics, the “grammar of graphics” (Wilkinson 2005). This makes ggplot2 very powerful because it provides a language for succintly translating statistical ideas directly onto graphs. On the other hand, the significant departure of ggplot2 from traditional graphics models can make its learning curve somewhat harder, especially if you’re used to traditional graphics models.

The ggplot2 book by Wickham (2009) is the best reference for learning ggplot2. The draft of the third edition of the book is freely available here. Other useful resources include ggplot2 tutorial by Josef Fruehwald, which is one of the best introductions to ggplot2 I’ve come across. A more recent version of this tutorial is available here.

All the examples in this chapter assume that ggplot2 has been installed and is loaded in your R session. If not, you can install it with:

install.packages("ggplot2")

and load it with:

library(ggplot2)

At its essence a plot is a mapping of certain properties of the data to certain visual properties of the medium (paper, screen, etc…) on which it appears. For example, a variable such as blood pressure, may be mapped to the coordinate of a point in the y axis, and another variable such as time, may be mapped to the coordinate of a point on the x axis. Sometimes variables may be mapped to other graphical aspects, such as the color of points, the type (solid, dashed, etc…) of a line, or the size of a point. ggplot2 implements a “grammar” of graphics that allows you to express and control this mappings with a high-level language. Compared to traditional plotting systems (such as base R graphics) this typically allows you to express these mappings concisely; if you master the grammar it may also allow to do it more quickly.

Two basic elements of ggplot2 are aesthetics, and geometries. Aesthetics in ggplot2 define the ways in which data properties are conceptually mapped to graphical elements (e.g. by position, color, shape, size, etc…). Geometries, on the other hand, represent the actual geometrical elements (e.g. points, lines, bars, etc…) used to implement these mappings. Let’s move on to some examples to clarify this. For these examples we’ll use the trees built-in R dataset, which contains measurements of the diameter, height and volume of 31 black cherry trees:

data(trees)
head(trees)

##   Girth Height Volume
## 1   8.3     70   10.3
## 2   8.6     65   10.3
## 3   8.8     63   10.2
## 4  10.5     72   16.4
## 5  10.7     81   18.8
## 6  10.8     83   19.7

the documentation for the dataset (see ?trees) tells us that the diameter (in inches) was erroneously labelled “Girth” in the data, so we’ll correct the column name in the dataset:

trees = trees %>% rename(Diameter=Girth)

We can visualize the diameter and height data, and their relation, by mapping the diameter to position on the x axis, and the height to position on the y axis, then use points to implement these mapping. In ggplot2 we would write:

ggplot(data=trees, mapping=aes(x=Diameter, y=Height)) + geom_point()

Figure 7.1: Diameter and height of 31 black cherry trees.

the resulting plot is shown in Figure 7.1. Note how the ggplot function takes two arguments, data must be a dataframe holding the variables of interest; the mapping argument takes a function called aes that specifies the aesthetic mappings. The geometry is “added” later with the + operator. From now on we will omit for brevity the argument names and simply write:

ggplot(trees, aes(x=Diameter, y=Height)) + geom_point()

One way to map the data on the volume of the trees onto the current graph could be to vary the size of the points depending on the volume:

ggplot(trees, aes(x=Diameter, y=Height, size=Volume)) + geom_point()

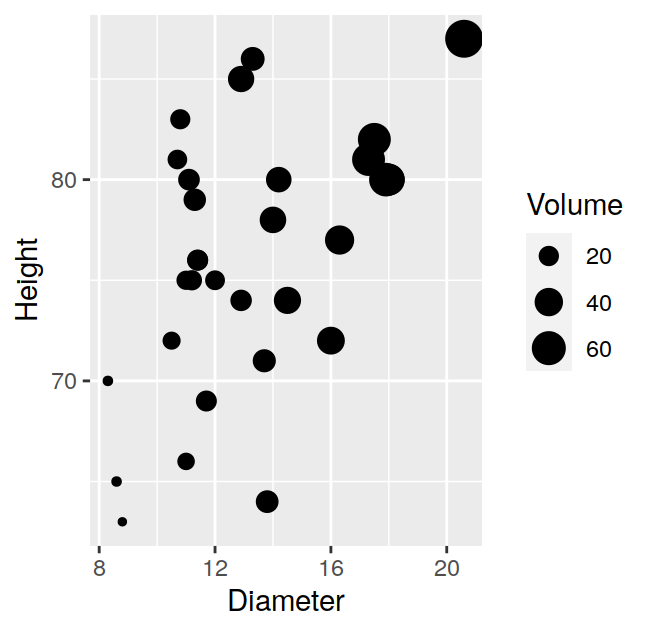
Figure 7.2: Diameter, height, and volume of 31 black cherry trees. The volume of the trees is represented by the size of the plotting points.

the resulting plot is shown in Figure 7.2. Yet another way to map the data on the volume of the trees onto the plot could be to set the color of the points depending on the value of the volume:

ggplot(trees, aes(x=Diameter, y=Height, color=Volume)) + geom_point()

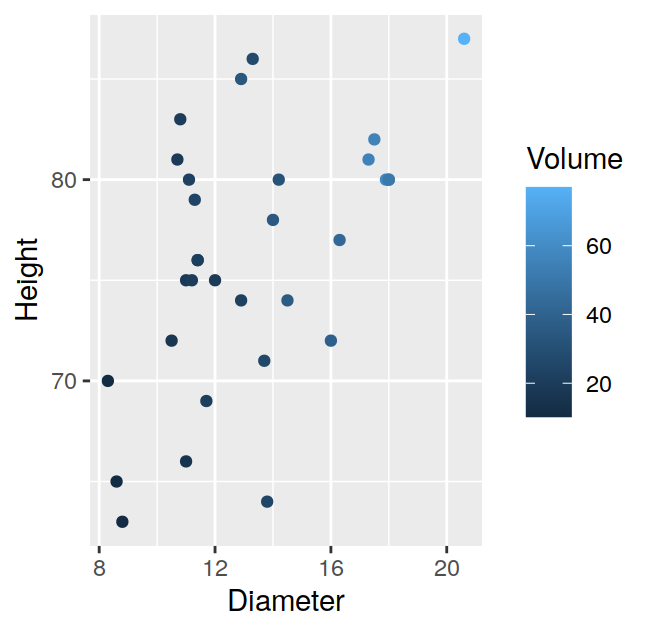
Figure 7.3: Diameter, height, and volume of 31 black cherry trees. The volume of the trees is represented by the color of the plotting points.

The resulting plot is shown in Figure 7.3. for this last plot we may want to increase the size of all points to make their color easier to see. We can do this by passing a size argument to geom_point (plot shown in Figure 7.4):

ggplot(trees, aes(x=Diameter, y=Height, color=Volume)) + geom_point(size=3)

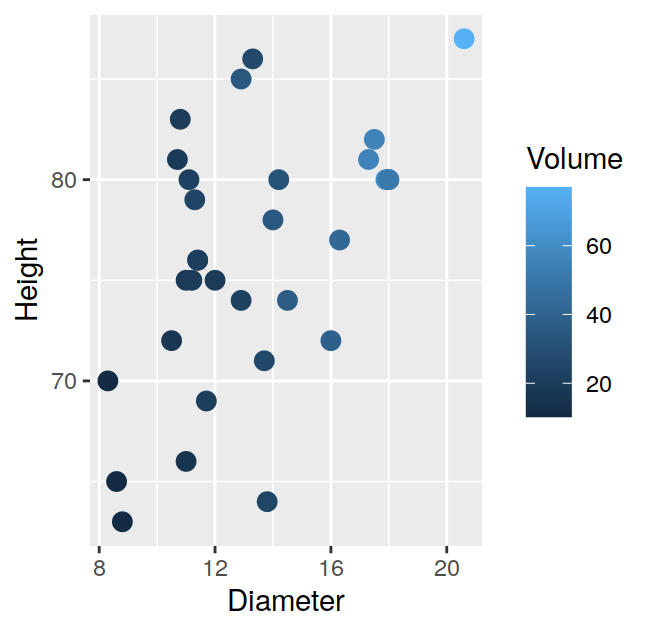
Diameter, height, and volume of 31 black cherry trees. The volume of the trees is represented by the color of the plotting points. The points have been set to a relatively large size to make it easier to see their color.

Figure 7.4: Diameter, height, and volume of 31 black cherry trees. The volume of the trees is represented by the color of the plotting points. The points have been set to a relatively large size to make it easier to see their color.

although by doing this we are modifying an aesthetic quality of the plot, this does not generate an aesthetic mapping between the data and the graphic in the sense of the grammar of graphics.

Aesthetic mappings always go within an aes call, while changes of the visual properties of the plot that are not aesthetic mappings go outside aes calls.

Check what happens if we pass the call to change the size of all the points (not an aesthetic mapping) inside the aes:

# wrong!
ggplot(trees, aes(x=Diameter, y=Height, color=Volume, size=3)) + geom_point()

Some common aesthetics are listed in Table 7.1, while Table 7.2 lists some common geometries.

Table 7.1: Common `ggplot2` aesthetics.
Aesthetic
`color`
`fill`
`shape`
`size`
`linetype`

Table 7.2: Common `ggplot2` geometries.
Geometry
`geom_point`
`geom_line`
`geom_path`
`geom_bar`
`geom_col`
`geom_errorbar`
`geom_smooth`
`geom_hline`
`geom_vline`
`geom_abline`

7.1 Common charts

7.1.1 Scatterplots

We’ve already seen some scatterplots at the beginning of this chapter. We’ll show some new ones in this section using the iris dataset, which contains measurements of various physical properties of 150 flowers from three different species of iris:

data(iris)
head(iris)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

We’ll start with a scatterplot of petal length by petal width (shown in Figure 7.5):

p = ggplot(iris, aes(Petal.Width, Petal.Length)) + geom_point()
p = p + xlab("Petal Width (cm)") + ylab("Petal Length (cm)")
p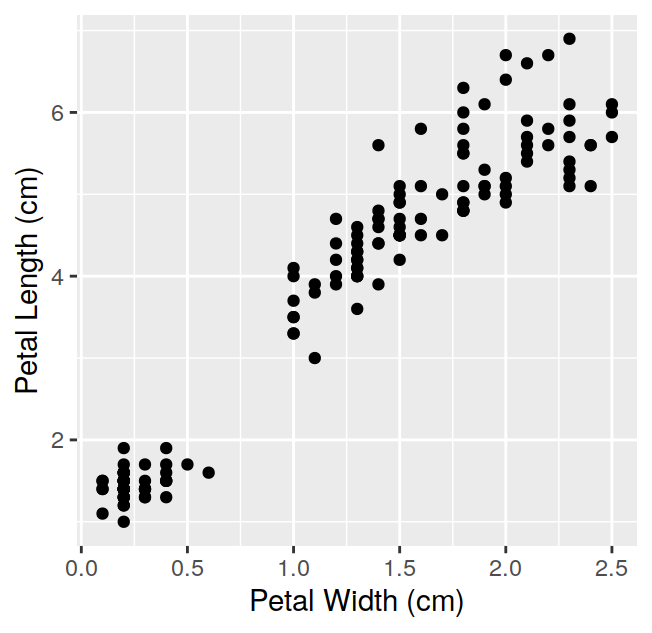

Figure 7.5: Scatterplot of petal length by petal width for the iris dataset.

Next we’ll map the species of each flower to color (plot shown in Figure 7.6):

p = ggplot(iris, aes(Petal.Width, Petal.Length, color=Species)) + geom_point()
p = p + xlab("Petal Width (cm)") + ylab("Petal Length (cm)")
p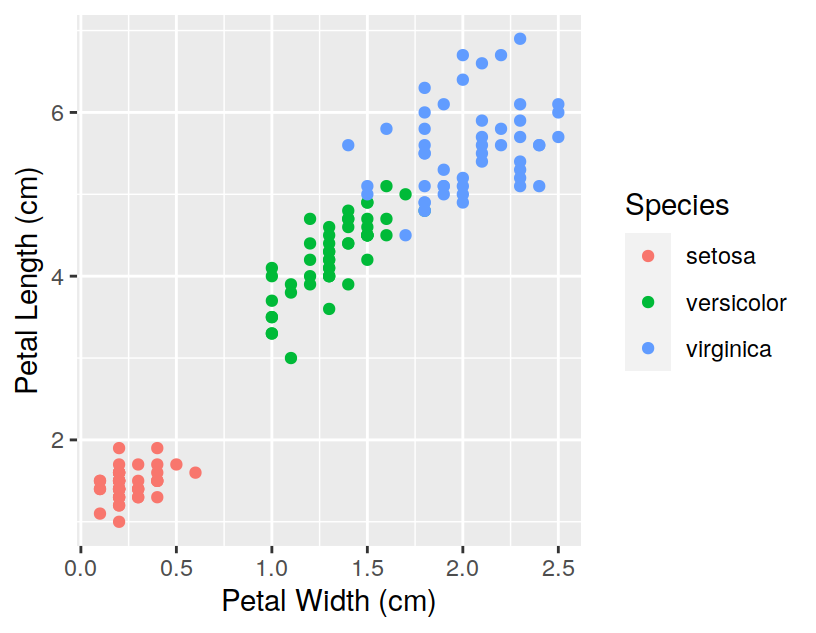

Figure 7.6: Scatterplot of petal length by petal width for the iris dataset. Species is mapped to color.

7.1.2 Time series

We’ll plot a time series using the Orange built-in R datasets, which contains data on the growth of five orange trees. The result can be seen in Figure 7.7.

p = ggplot(Orange, aes(age, circumference, color=Tree)) + geom_point()
p = p + geom_path()
p = p + xlab("Age (days)") + ylab("Circumference (mm)")
p

Figure 7.7: Growth of orange trees: trunk circumference by age (in days) for five trees.

7.1.3 Barplots

For the following examples we’ll use the npk dataset, which contains data from a factorial experiment on the effects of N, P, K (nitrogen, phosphate, potassium) on the growth of peas.

data(npk)
head(npk)

##   block N P K yield
## 1     1 0 1 1  49.5
## 2     1 1 1 0  62.8
## 3     1 0 0 0  46.8
## 4     1 1 0 1  57.0
## 5     2 1 0 0  59.8
## 6     2 1 1 1  58.5

in the dataset N, P, and K are indicator variables for the application of the respective element (0=no, 1=yes). We’ll first plot the mean yield as a function of N, averaging across the levels of the other factors. In order to do this we’ll generate a summary data set:

npk_summ_N = npk %>% group_by(N) %>% summarize(mean_yield=mean(yield),
                                               sd_yield=sd(yield))

the barplot can be generated using geom_col (plot shown in Figure 7.8):

p1 = ggplot(npk_summ_N, aes(N, mean_yield)) + geom_col()
p1 = p1 + ylab("Mean yield")
p1

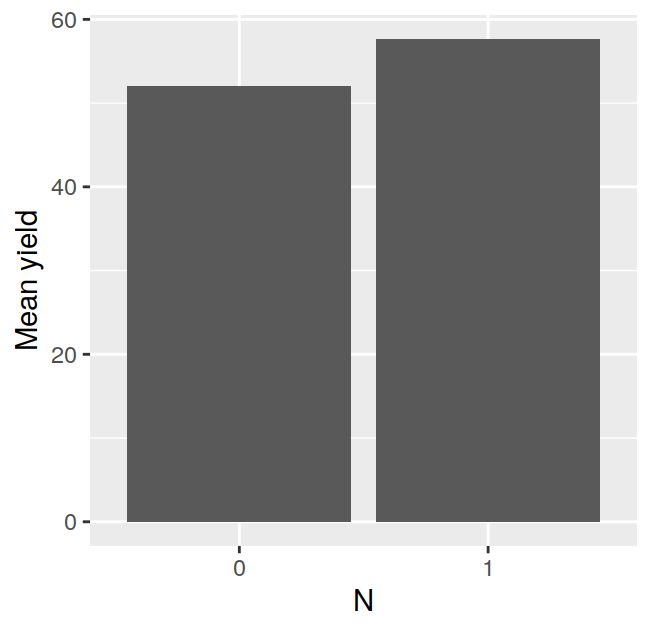
Figure 7.8: Yield as a function of nitrogen application.

we can add error bars showing the standard deviation using geom_errorbar (plot shown in Figure 7.9):

p1e = ggplot(npk_summ_N, aes(N, mean_yield)) + geom_col()
p1e = p1e + geom_errorbar(aes(ymin=mean_yield-sd_yield,
                              ymax=mean_yield+sd_yield),
                          width=0.2)
p1e = p1e + ylab("Mean yield")
p1e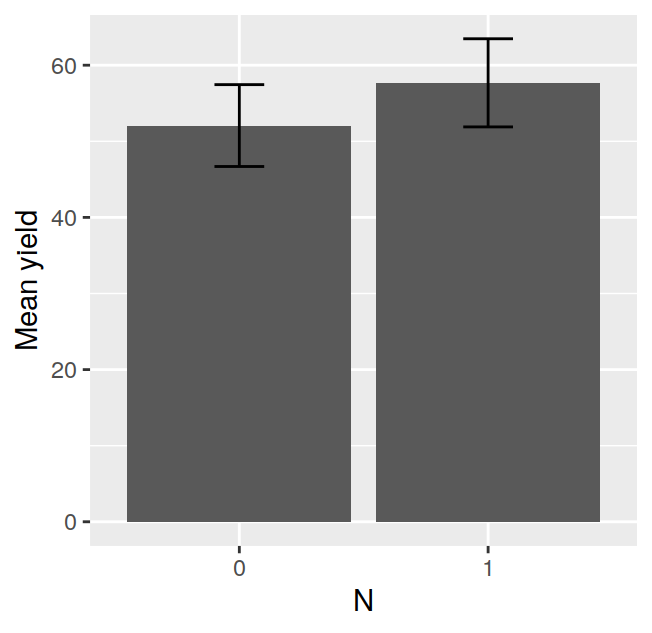

Figure 7.9: Yield as a function of nitrogen application.

Next, we’ll plot the mean yield as a function of both N and P. We first generate a summary dataset as a function of both N and P with:

npk_summ_NP = npk %>% group_by(N,P) %>% summarize(mean_yield=mean(yield),
                                                  sd_yield=sd(yield))

and then generate the barplot (shown in Figure 7.10):

p2 = ggplot(npk_summ_NP, aes(N, mean_yield, fill=P))
p2 = p2 + geom_col()
p2 = p2 + ylab("Mean yield")
p2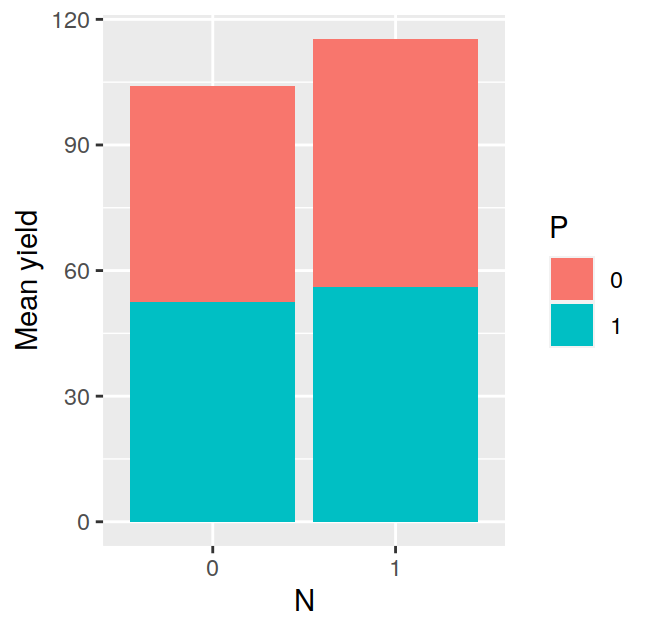

Figure 7.10: Stacked barplot showing yield as a function of nitrogen and phosphate application.

the code above generates a stacked barplot. To generate a barplot with the bars “side to side” rather than stacked on top of each other we have to use position_dodge to offset the position of the bars relative to each other:

dodge_size = 0.9
p2d = ggplot(npk_summ_NP, aes(N, mean_yield, fill=P))
p2d = p2d + geom_col(position=position_dodge(dodge_size))
p2d = p2d + geom_errorbar(aes(ymin=mean_yield-sd_yield,
                              ymax=mean_yield+sd_yield),
                          position=position_dodge(dodge_size),
                          width=0.2)
p2d = p2d + scale_fill_manual(name="P", values=palette()[c(2,4)])
p2d = p2d + ylab("Mean yield")
p2d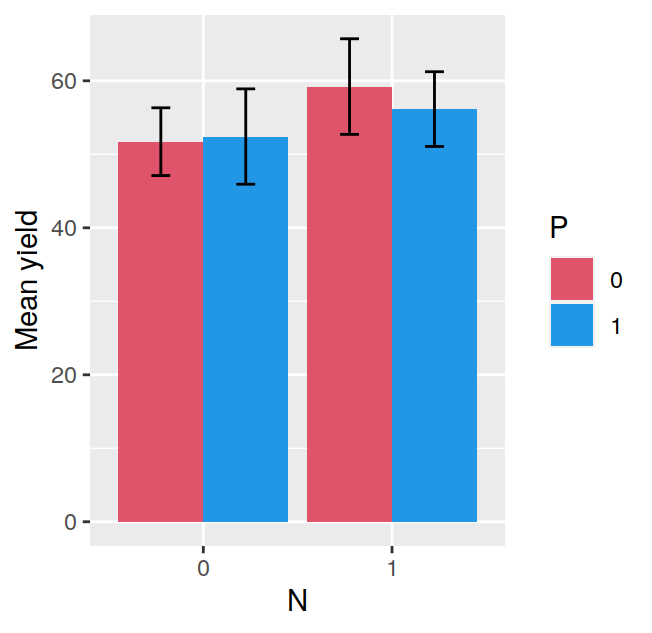

Figure 7.11: Barplot with bars side by side showing yield as a function of nitrogen and phosphate application.

the resulting plot is shown in Figure 7.11. Again we added some error bars; note how we had to set the position argument also for geom_errorbar to make sure the error bars are aligned to the bars of the barplot. We also changed the colors of the bars with scale_fill_manual.

We can visualize the effect of all three factors (N, P, K) by showing mean values of K along different panels. We’ll first generate a summary dataset as a function of all three factors:

npk_summ_NPK = npk %>% group_by(N,P,K) %>% summarize(mean_yield=mean(yield),
                                                     sd_yield=sd(yield))

and then generate the plot (shown in Figure 7.12):

p3 = ggplot(npk_summ_NPK, aes(N, mean_yield, fill=P))
p3 = p3 + geom_col(position=position_dodge(dodge_size))
p3 = p3 + facet_wrap(~K)
p3 = p3 + geom_errorbar(aes(ymin=mean_yield-sd_yield,
                              ymax=mean_yield+sd_yield),
                          position=position_dodge(dodge_size),
                          width=0.2)
p3 = p3 + scale_fill_manual(name="P", values=palette()[c(2,4)])
p3 = p3 + ylab("Mean yield")
p3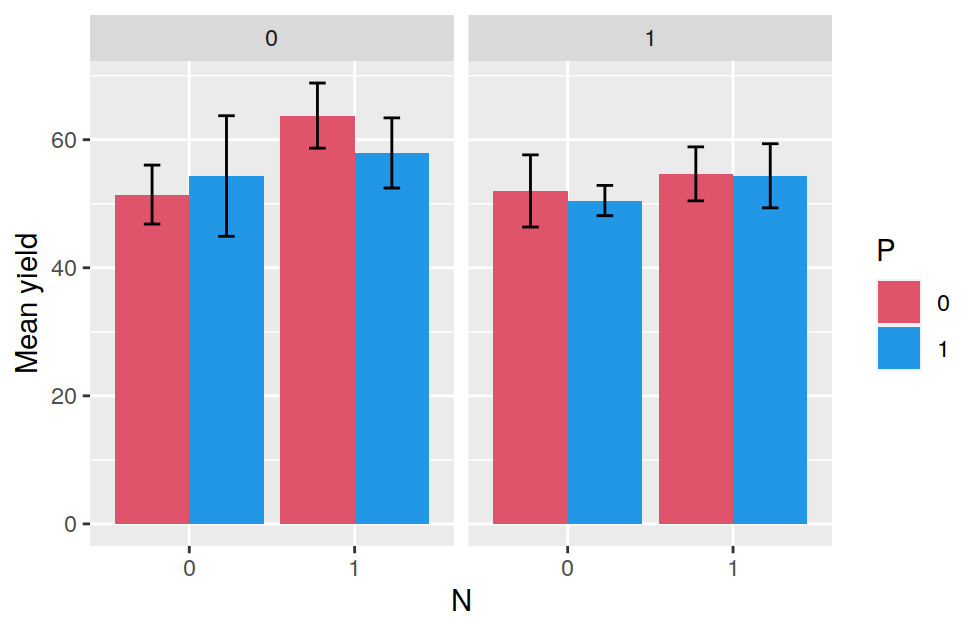

Barplot showing yield as a function of nitrogen and phosphate application. Panels plot mean yield as a function of the application of potassium (0=no, 1=yes).

Figure 7.12: Barplot showing yield as a function of nitrogen and phosphate application. Panels plot mean yield as a function of the application of potassium (0=no, 1=yes).

Besides geom_col there is a geom_bar that can generate barplots. This geometry, combined with the “identity” stat (geom_bar(stat="identity")) will produce the same plot as geom_col. However, the default stat for geom_bar is count, so it will plot the count of cases of a certain factor. For example Figure 7.13 plots the number of cars for each manufacturer in the mpg dataset, and was obtained with the code below:

data(mpg)
p = ggplot(mpg, aes(manufacturer)) + geom_bar()
p = p + theme(axis.text.x = element_text(angle = 45, hjust = 1))
p

Figure 7.13: Number of cars by manufacturer in the mpg dataset.

Figure 7.14 instead, plots the number of cars by manufacturer and type of transmission, and was obtained with the following code:

p = ggplot(mpg, aes(manufacturer, fill=trans))
p = p + geom_bar(position=position_dodge(0.9))
p = p + theme(axis.text.x = element_text(angle = 45, hjust = 1))
p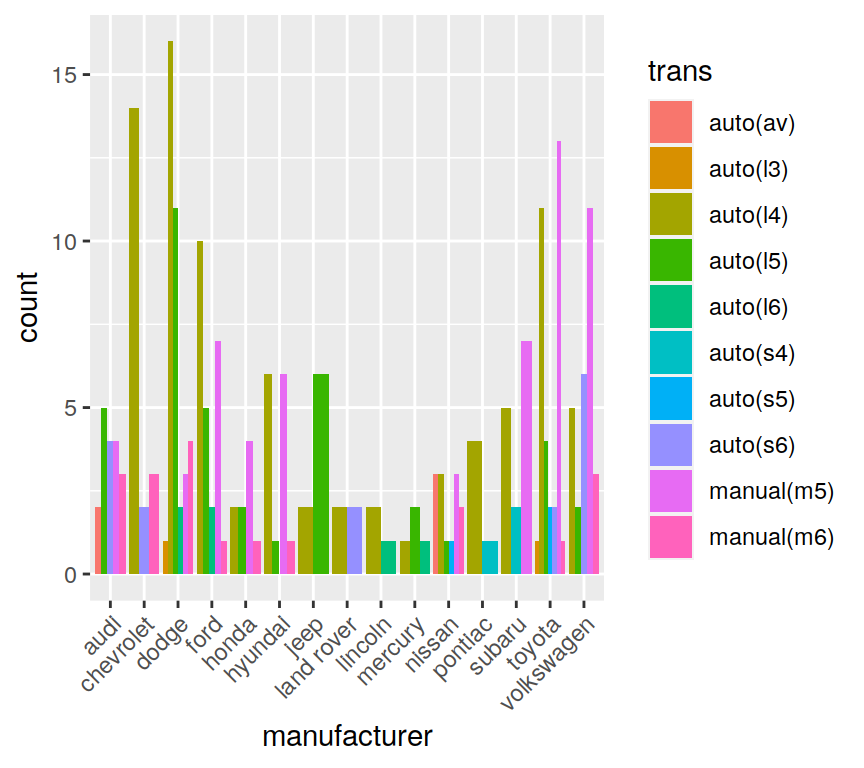

Figure 7.14: Number of cars by manufacturer and type of transmission in the mpg dataset.

7.1.4 Interaction plots

For the next example we’ll use the ToothGrowth built-in R dataset, which contains measurements of the length of odontoblasts (cells responsible for tooth growth) in 60 guinea pigs. Each guinea pig had received one of three doses of vitamin C (0.5, 1, and 2 mg/day) by one of two delivery methods, orange juice (OJ) or ascorbic acid (VC).

data(ToothGrowth)
head(ToothGrowth)

##    len supp dose
## 1  4.2   VC  0.5
## 2 11.5   VC  0.5
## 3  7.3   VC  0.5
## 4  5.8   VC  0.5
## 5  6.4   VC  0.5
## 6 10.0   VC  0.5

we’ll first generate a summary dataset as a function of delivery method (supp variable), and dose:

ToothGrowthSumm = ToothGrowth %>% group_by(supp, dose) %>%
                                  summarize(meanLen=mean(len))
ToothGrowthSumm$dose = factor(ToothGrowthSumm$dose)

now we can generate the plot (shown in Figure 7.15) with the following code:

p = ggplot(ToothGrowthSumm, aes(x=supp, y=meanLen,
                                shape=dose, linetype=dose, group=dose))
p = p + geom_point()
p = p + geom_line()
p = p + theme_classic()
p = p + scale_shape_discrete(name="Dose")
p = p + scale_linetype_discrete(name="Dose")
p = p + xlab("Delivery method")
p = p + ylab("Mean growth")
p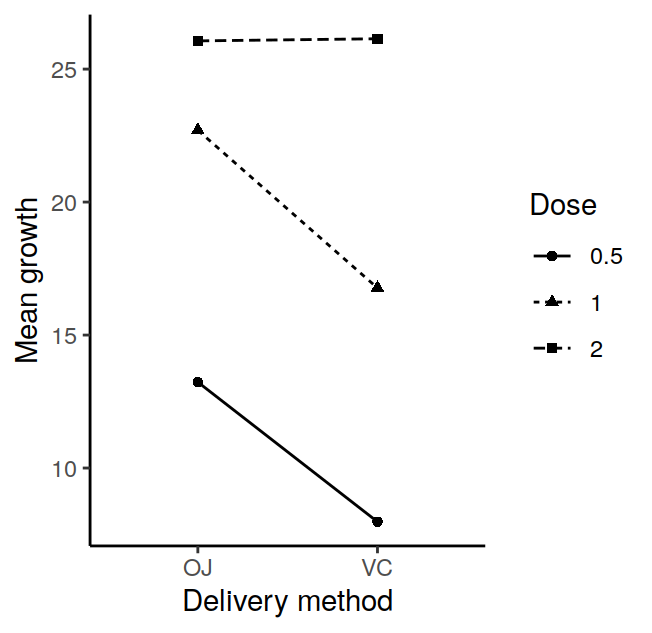

Figure 7.15: Tooth growth by vitamin C dose and delivery method in guinea pigs.

7.2 Scales

7.2.1 Log axis with pretty tickmarks

The annotation_logticks function can be used to generate “pretty” tickmarks for axes on a log10 scale. An example is given in the code below (plot shown in Figure 7.16):

x = c("cnd1", "cnd2")
y = c(0.4, 80)

dat = data.frame(x=x, y=y)

p = ggplot(dat, aes(x=x, y=y)) + geom_point()
p = p + scale_y_continuous(trans="log10")
p = p + annotation_logticks(sides="l")
p = p + theme_bw(base_size=12)
p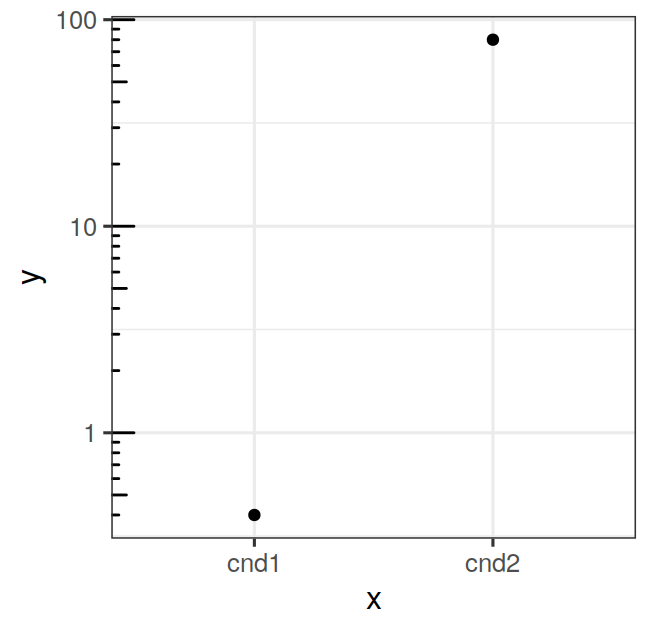

Figure 7.16: Log axis with pretty tickmarks

7.3 Themes

ggplot2 ships with a number of themes included. The ggthemes package provides a number of additional themes.

7.4 Tips and tricks

7.4.1 Fixing labels that won’t fit

Sometimes an axis label may be clipped off as in the next example:

set.seed(260420)
y=rnorm(3)
dd = data.frame(x=c("Effect of first condition A",
                    "Effect condition B",
                    "Effect condition C"),
                y=y, lower=y-runif(3, 0.5, 1),
                upper=y+runif(3, 0.5, 1))
p = ggplot(dd, aes(x,y)) + geom_point(shape=1)
p = p + geom_errorbar(aes(ymin=lower, ymax=upper), width=0)
p = p + coord_flip() + theme_bw() + xlab(NULL)
p = p + ylab("A really long label that won't easily fit!")
p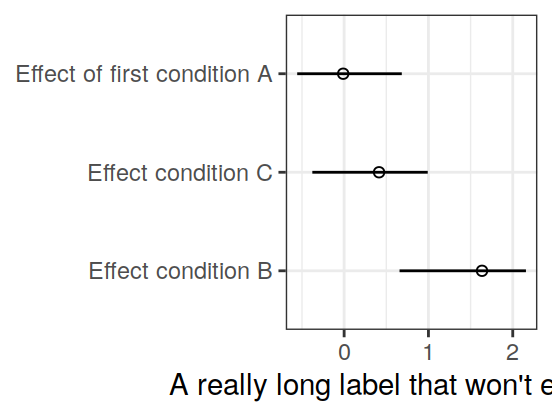

Figure 7.17: Example of axis label tha doesn’t fit

the label can be shifted by changing the value of hjust for the element_text or the axis.title.x:

p = p + theme(axis.title.x = element_text(hjust=1))
p

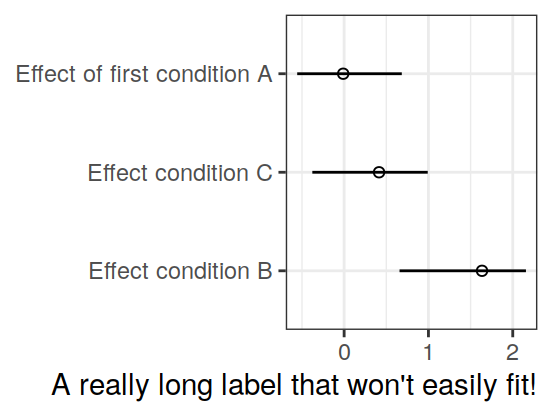
Figure 7.18: Fitting a long label with hjust

alternatively we can use the draw_label function from the cowplot package to fine tune the label position:

library(cowplot)
p = ggplot(dd, aes(x,y)) + geom_point(shape=1)
p = p + geom_errorbar(aes(ymin=lower, ymax=upper), width=0)
p = p + coord_flip() + theme_bw() + xlab(NULL)
p = p + ylab("")
p = ggdraw(p) + draw_label("A really long label that won't easily fit!",
                           x = 0.025, y = 0.1, hjust = 0, vjust = 1,
                           size = 12)
p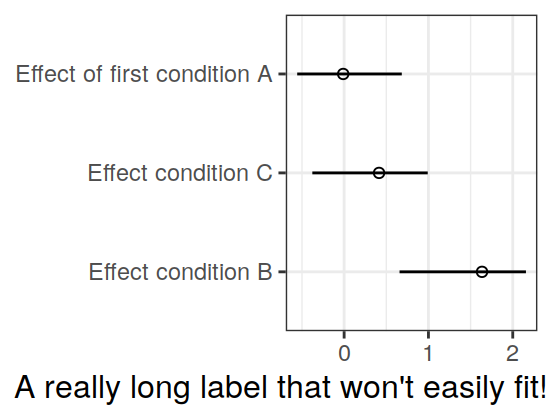

Figure 7.19: Fitting a long label with draw_label from cowplot

7.4.2 Setting the aspect ratio

In the following plot (Figure 7.20) the x and y variables are roughly on the same scale, but we’ve purposefully added an outlier so that the two axes have different ranges:

x = rnorm(100) #simulate data
y = rnorm(100)
y[1] = y[1] + 10 #add outlier
dat = data.frame(x=x, y=y)
p = ggplot(dat, aes(x, y)) + geom_point()
p = p + geom_abline(slope=1, intercept=0)
p = p + theme_bw()
p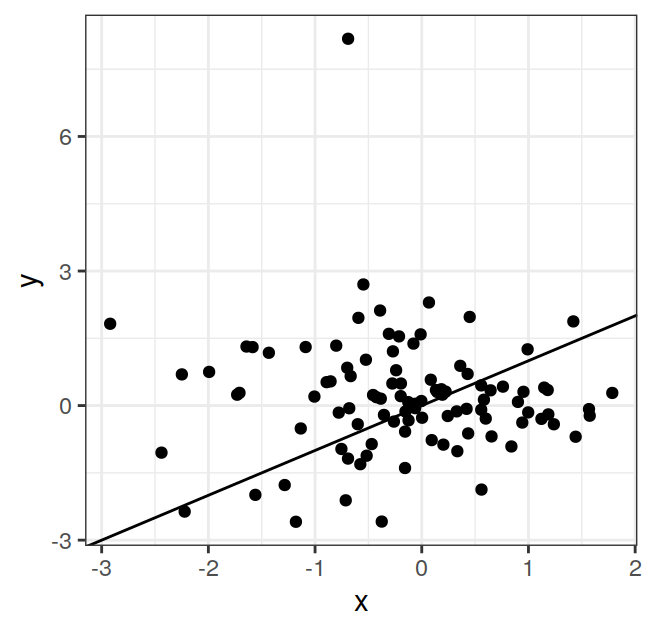

Figure 7.20: A scatterplot. The aspect ratio is not fixed.

we can set the aspect ratio to 1 with p = p + coord_fixed(ratio=1):

p = p + coord_fixed(ratio=1)
p

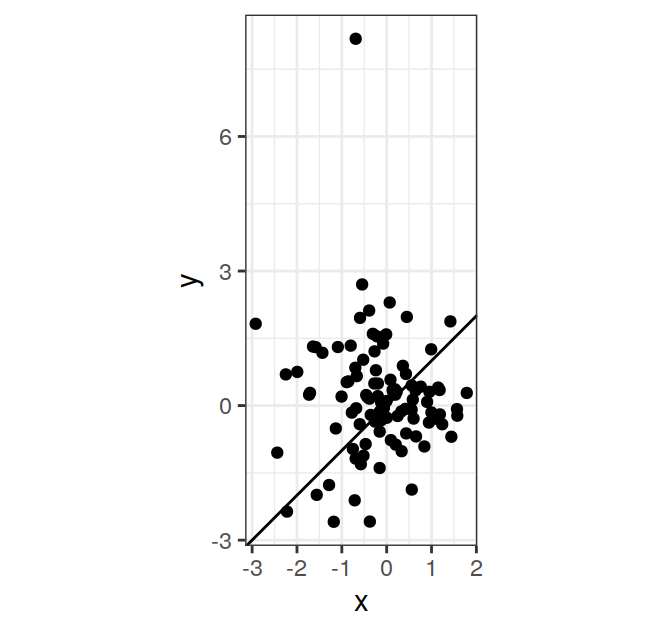
Figure 7.21: A scatterplot with aspect ratio fixed to 1.

this fixes the aspect ratio to 1, but the plot, shown in Figure 7.21, looks somewhat odd because it is not square. To fix this we need to calculate the ranges of both axes and set them at their max/min:

p = ggplot(dat, aes(x, y)) + geom_point()
p = p + geom_abline(slope=1, intercept=0)
xmax = max(layer_scales(p)$x$range$range)
ymax = max(layer_scales(p)$y$range$range)
xymax = max(xmax,ymax)
xmin = min(layer_scales(p)$x$range$range)
ymin = min(layer_scales(p)$y$range$range)
xymin = min(xmin,ymin)
p = p + coord_equal(xlim=c(xymin,xymax), ylim=c(xymin,xymax))
p = p + theme_bw()
p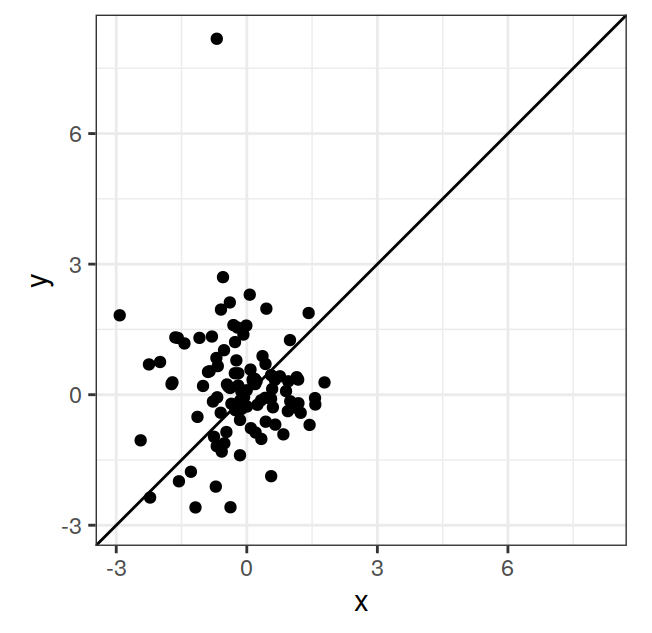

Figure 7.22: A scatterplot with aspect ratio fixed to 1, and a square plotting area.

in this way we obtain the plot shown in Figure 7.22, which looks better.

7.5 Further resources

7.5.1 Books, articles, and tutorials

Creating publication quality graphs in R by Tim Appelhans, provides useful notes on both lattice and ggplot2, including ways to manipulate and arrange plots using grid. The git repository of the tutorial is available here.

8 Plotly

Figures in this section may not appear in the pdf version of the book. Please use the html version if that is the case: https://sam81.github.io/r_guide_bookdown/rguide.html

The “plotly for R” book (Sievert 2020) is the best introduction for learning plotly.

We’ll start by loading plotly and generating some random data for a scatterplot:

library(plotly)
x = rnorm(10); y=rnorm(10)

we can now generate a scatterplot, which is shown in Figure 8.1:

plot_ly(x=x, y=y, type="scatter", mode="markers")

## Warning: `arrange_()` is deprecated as of dplyr 0.7.0.
## Please use `arrange()` instead.
## See vignette('programming') for more help
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_warnings()` to see where this warning was generated.

Figure 8.1: Plotly example.

we can change the color, size and opacity of the plotting points, obtaining the plot shown in Figure 8.2:

plot_ly(x=x, y=y, type="scatter", mode="markers",
        marker=list(color="black" , size=15 , opacity=0.8))

Figure 8.2: Plotly example.

8.1 `ggplotly`

The ggplotly function can be used to convert a ggplot2 graphic into an interactive plotly graphic. For example, the following code generates Figure 8.3:

p = ggplot(iris, aes(Sepal.Width, Sepal.Length, color=Species)) + geom_point()
p = p + xlab("Sepal width") + ylab("Sepal length")
ggplotly(p)

Figure 8.3: ggplotly example.

While the conversion is smooth for simple plots, your mileage may vary with more complex plots. Work is ongoing to improve the conversion process, and hopefully in the future ggplotly will be able to seamlessly convert any ggplot2 graphic seamlessly to interactive plotly graphics. In the meantime, you just have to try it to check whether the conversion works for a specific plot you might need.

8.2 Using plotly with knitr

Plotly figures are rendered directly in the html output with knitr:

```{r chunk-label, fig.cap = 'A figure caption.'}
plot_ly(economics, x = ~date, y = ~unemploy / pop)
```

please note that if the plot is assigned to a variable you need to call that variable in the code chunk for the plot to be rendered:

```{r chunk-label, fig.cap = 'A figure caption.'}
p = plot_ly(economics, x = ~date, y = ~unemploy / pop)
p #call the variable storing the plot to render it
```

Plotly figures can also appear in pdf files generate by knitr if the webshot package is installed. Besides this package, you will also need to have PhantomJS (http://phantomjs.org/) installed on your system. You can install both webshot and PhantomJS from within R with the following commands:

install.packages("webshot")
webshot::install_phantomjs()

9 Lattice graphics

The lattice package provides an alternative to the base R graphics system; it is an implementation of the ideas developed and implemented mainly by Rick Becker and Bill Cleveland in the Trellis graphics system for the S language (Adler 2010; Crawley 2013). Trellis displays were developed as a framework to easily display of the relationship between a dependent variable and multiple factors.

The best introduction to lattice graphics is the book by Sarkar (2008), the author of lattice. The lattice package documentation, available here, is a good reference. The articles of Sarkar (2002), Sarkar (2003), and the book chapter of Murrell (2001) are good introductory resources.

Because lattice is mostly compatible with the Trellis graphics system in S-Plus, articles/documents written for Trellis (e.g. Becker et al. 1996; Becker, Cleveland, and Shyu 1996; Cleveland and Fuentes 1997; Becker and Cleveland 2002), also provide a good introduction to lattice and to the concept of trellis displays.

9.1 Overview of lattice graphics

Table 9.1 lists some of the most common high-level lattice plotting functions. We’ll look at some of these in the following sections, but first we’ll describe the model formulae system used by lattice and introduce the concept of multi-panel conditioning in the next section.

Table 9.1: Some high-level plotting functions in `lattice`.
Function	Chart types
`xyplot`	scatterplot, time-series, interaction plot
`barchart`	barplot
`dotplot`	dotplot
`stripplot`	stripplot
`bwplot`	box-and-whisker

9.2 Introduction to model formulae and multi-panel conditioning

To illustrate how conditioning on one or more factors works in lattice we’ll use the npk dataset, which contains data from a factorial experiment on the effects of N, P, K (nitrogen, phosphate, potassium) on the growth of peas:

data(npk)
npk$P = factor(npk$P, levels=c("0", "1"), labels=c("P=0", "P=1"))
npk$K = factor(npk$K, levels=c("0", "1"), labels=c("K=0", "K=1"))

in the dataset N, P, and K are indicator variables for the application of the respective element (0=no, 1=yes). We renamed the levels of the P and K factors to make legends and strip labels easier to read. We’ll first plot the mean yield as a function of N, averaging across the levels of the other factors. In order to do this we’ll generate a summary data set:

library(dplyr)
npk_summ_N = npk %>% group_by(N) %>% summarize(mean_yield=mean(yield),
                                               sd_yield=sd(yield))

Two basic elements of lattice plots consist of a dataframe, and a model formula specifying how you want a given variable to be displayed along the dimensions of one or more factors. In our case, we want mean_yield ~ N (you could read the ~, “as a function of”), the barchart can be produced with the code below, and is displayed in Figure 9.1:

library(lattice)
##trellis.device() #optional opens an X11() window on Linux
pl1 = barchart(mean_yield ~ N, data=npk_summ_N,
               xlab="N", ylab="Mean yield")
print(pl1)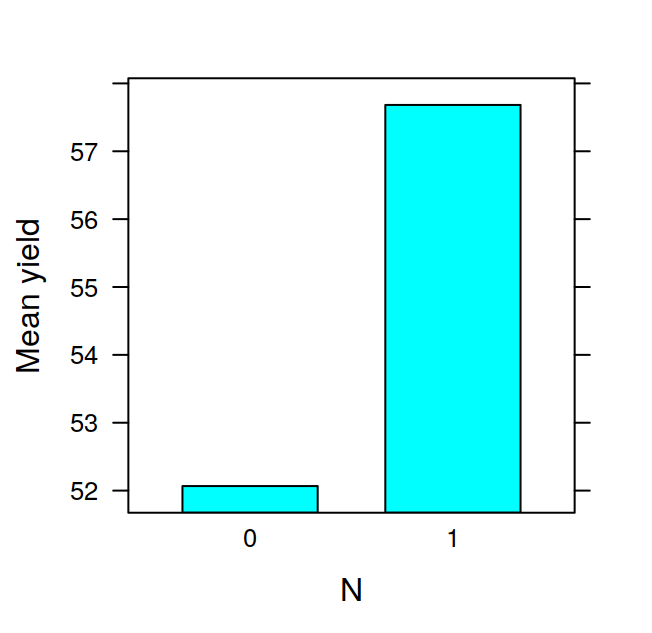

Figure 9.1: Yield as a function of nitrogen application.

Now suppose we want to visualise the relation between yield and N depending on P administration. In lattice there are two ways of doing it, one is by the use of a “grouping” factor. The second way is by multi-panel factor conditioning. The advantage of multi-panel conditioning, as we will see soon, is that it can be extended to an unlimited number of factors. Let’s start with the first solution, in which we use a grouping factor. We first generate a summary dataset as a function of both N and P with:

npk_summ_NP = npk %>% group_by(N,P) %>% summarize(mean_yield=mean(yield),
                                                  sd_yield=sd(yield))

and then generate the barplot (shown in Figure 9.2):

pl2 = barchart(mean_yield ~ N, groups=P, 
               data=npk_summ_NP, auto.key=TRUE,
               xlab="N", ylab="Mean yield")
print(pl2)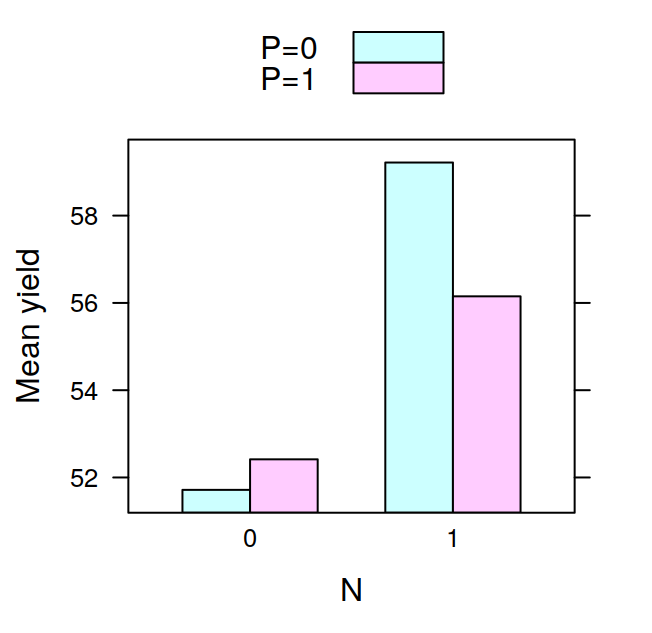

Figure 9.2: Barplot with bars side by side showing yield as a function of nitrogen and potassium application.

the grouping factor is given by the groups argument, note also that we have set auto.key to TRUE in order to automatically add a legend.

The second way of building the graph is by multi-panel conditioning. We achieve this by setting P as a conditioning factor with the | operator. The model formula becomes mean_yield ~ N | P, which you could read as "mean yield as a function of N, given P`. The plot shown in Figure 9.3:

pl3 = barchart(mean_yield ~ N | P, data=npk_summ_NP,
               xlab="N", ylab="Mean yield")
print(pl3)

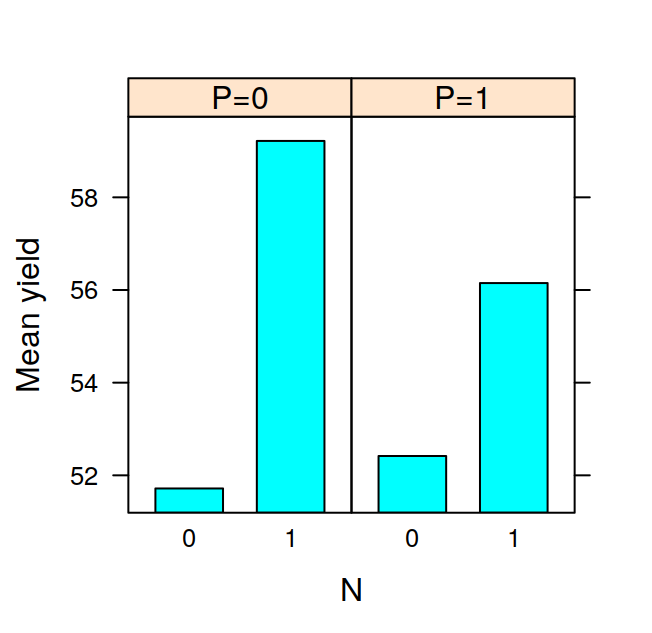
Figure 9.3: Barplot showing yield as a function of nitrogen and potassium application using multi-panel conditioning.

We can visualize the effect of all three factors (N, P, K) by showing mean values of K along different panels. We’ll first generate a summary dataset as a function of all three factors:

npk_summ_NPK = npk %>% group_by(N,P,K) %>% summarize(mean_yield=mean(yield),
                                                     sd_yield=sd(yield))

and then generate the plot (shown in Figure 9.4):

pl4 = barchart(mean_yield ~ N | P+K, data=npk_summ_NPK,
               xlab="N", ylab="Mean yield")
print(pl4)

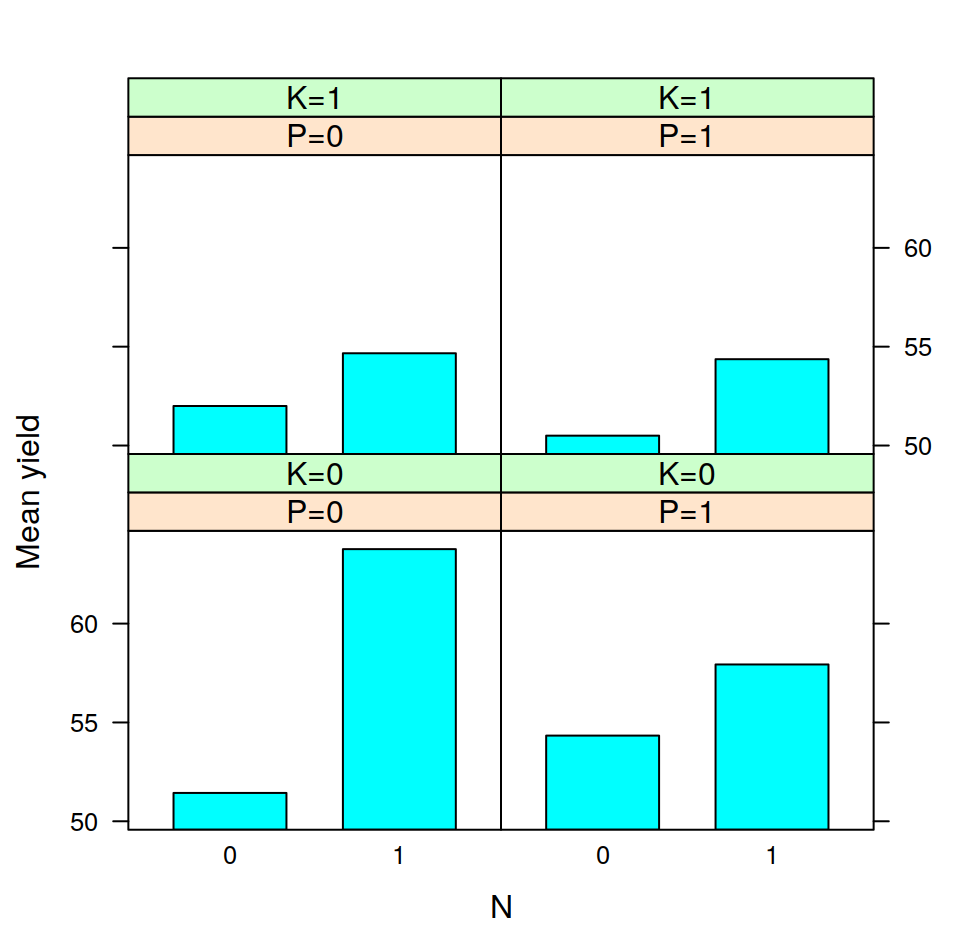
Barplot showing yield as a function of nitrogen and potassium application. Panels plot mean yield as a function of the application of phosphate (0=no, 1=yes).

Figure 9.4: Barplot showing yield as a function of nitrogen and potassium application. Panels plot mean yield as a function of the application of phosphate (0=no, 1=yes).

Also in this case we could have used a grouping variable rather than using two conditioning factors (Figure 9.5):

pl5 = barchart(mean_yield ~ N | P, groups=K, data=npk_summ_NPK,
               xlab="N", ylab="Mean yield", auto.key=T)
print(pl5)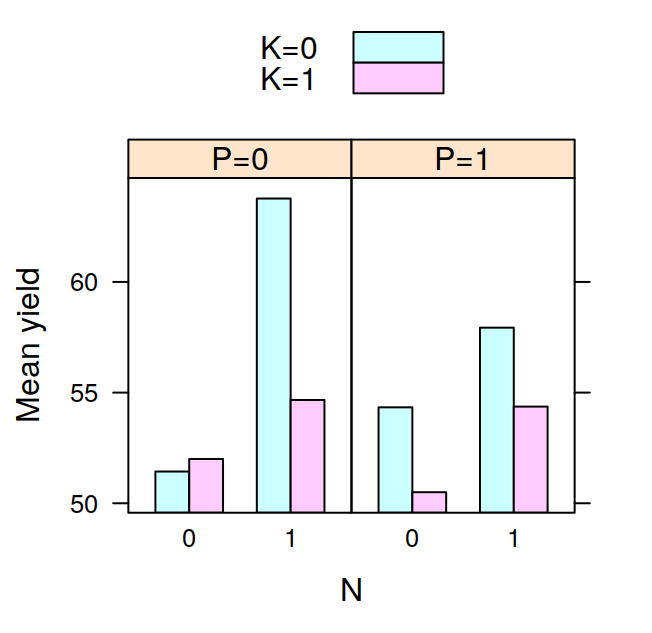

Barplot showing yield as a function of nitrogen, phosphate, and potassium application. Panels plot mean yield as a function of the application of potassium (0=no, 1=yes).

Figure 9.5: Barplot showing yield as a function of nitrogen, phosphate, and potassium application. Panels plot mean yield as a function of the application of potassium (0=no, 1=yes).

what is the best display is up to the user to decide, and depends from case to case.

9.3 Common charts

9.3.1 `xyplot`

The xyplot function can be used to generate scatterplots and time-series plots.

We’ll plot a scatterplot using the iris dataset (plot shown in Figure 9.6):

p = xyplot(Sepal.Length~Sepal.Width, groups=Species, data=iris, auto.key=T)
print(p)

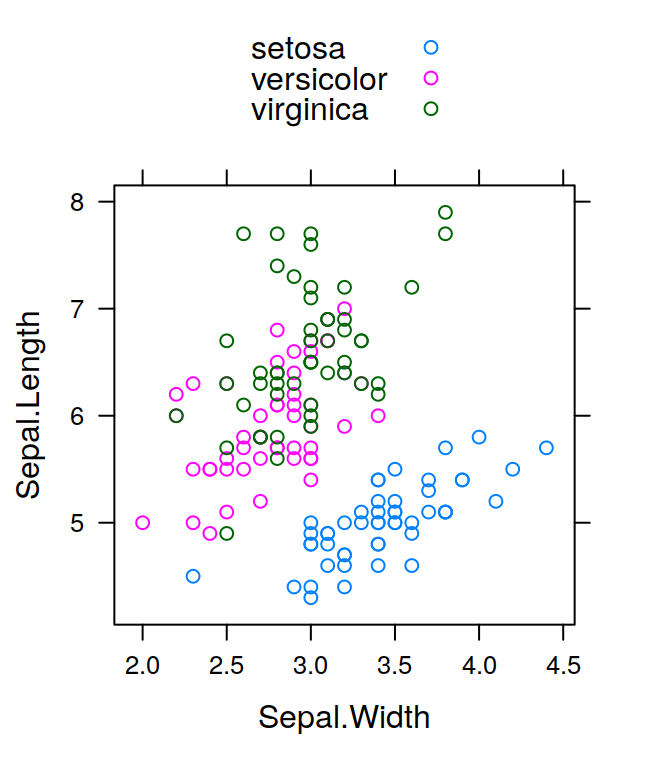
Figure 9.6: Scatterplot of sepal length by sepal width for the iris measurements in the iris dataset.

We can also obtain points connected by lines by passing the type="b" argument to xyplot. To illustrate this we’ll plot a time series using the Orange built-in R datasets, which contains data on the growth of five orange trees (plot shown in Figure 9.7):

xyplot(circumference~age, group=Tree, data=Orange,
       type="b", as.table=T,
       xlab="Age (days)", ylab="Circumference (mm)",
       auto.key=list(title="Tree", space="right"))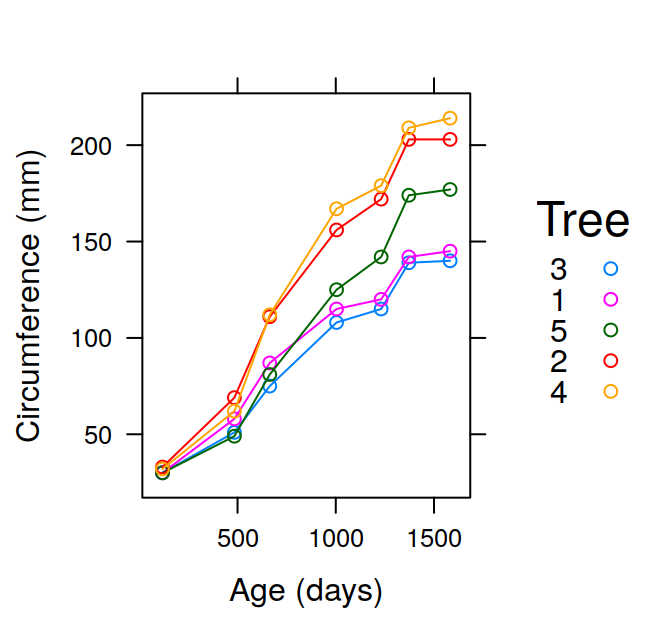

Figure 9.7: Growth of orange trees: trunk circumference by age (in days) for five trees.

9.3.2 `barchart`

We have already seen a few examples of barcharts built with lattice in Section 9.2. We’ll look at a few more examples in this section.

The following dataset contains both positive and negative values:

dat = data.frame(y=c(-0.5, 0.7, 1, -0.8),
                 fct1=c("A", "A", "B", "B"),
                 fct2 = c("1", "2", "1", "2")
                 )

in order to plot a barchart with bars going either up or down from a baseline value of zero we have to pass the argument origin=0. We’ll also change the fill color of the bars by changing the col attribute in the superpose.polygon list of settings (more info on setting graphical parameters in lattice are given in Section 9.4.1). The code for the barchart is shown below, the resulting plot is shown in Figure 9.8.

trellis.par.set(superpose.polygon = 
                    list(col = c("darkslateblue", "indianred"))
                )
p = barchart(y~fct1, origin=0, groups=fct2,
             data=dat)
print(p)

Figure 9.8: Barchart with origin set to zero.

9.3.3 Barcharts with error bars

There is no built-in support to add error bars to barcharts in lattice. This may be partly due to the fact that the lattice author thinks that barcharts with error bars are a bad data visualization choice (see discussion on R mailing list here).

Writing a custom panel function (see Section 9.5) for adding error bars to bar charts is complicated by the fact panel.barchart performs several calculations for placing the bars and the custom function needs to take them into account to work correctly. The code associated with this guide contains a file (barchart_errbar.R) with a modified barchart panel function that can draw error bars in some conditions. We’ll see how to use it shortly, but keep in mind that it may or may not work correctly, and that you should double check that it is doing the right thing! Also, it doesn’t work for horizontal barcharts.

For the following examples we’ll use the npk dataset, which we have introduced in Section 9.2. Again, we first generate a summary dataset with mean yield as a function of N with the code below:

data(npk)
npk$P = factor(npk$P, levels=c("0", "1"), labels=c("P=0", "P=1"))
npk$K = factor(npk$K, levels=c("0", "1"), labels=c("K=0", "K=1"))
npk_summ_N = npk %>% group_by(N) %>% summarize(mean_yield=mean(yield),
                                               sd_yield=sd(yield))
npk_summ_N$ci.l = npk_summ_N$mean_yield - npk_summ_N$sd_yield
npk_summ_N$ci.u = npk_summ_N$mean_yield + npk_summ_N$sd_yield

The last two lines of code add a ci.l and a ci.u column, which represent, respectively, the lower and upper limits of the error bars; we’ll use these two columns to add error bars to the plot. The code to draw the barchart with error bars is shown below:

source("code/barchart_errbar.R")
p1 = barchart(mean_yield~N, data=npk_summ_N,
              ci.l=npk_summ_N$ci.l, ci.u=npk_summ_N$ci.u,
              plot.ci=TRUE,
              auto.key=list(space="top", points=F, rectangles=T),
              prepanel=prepanel.barchart_errbar,
              panel=function(x,y, ci.l, ci.u, subscripts,...){
                  ci.l = ci.l[subscripts]
                  ci.u = ci.u[subscripts]
                  panel.barchart_errbar(x, y, ci.l=ci.l, ci.u=ci.u,
                                  subscripts=subscripts,...)
              }
              )
print(p1)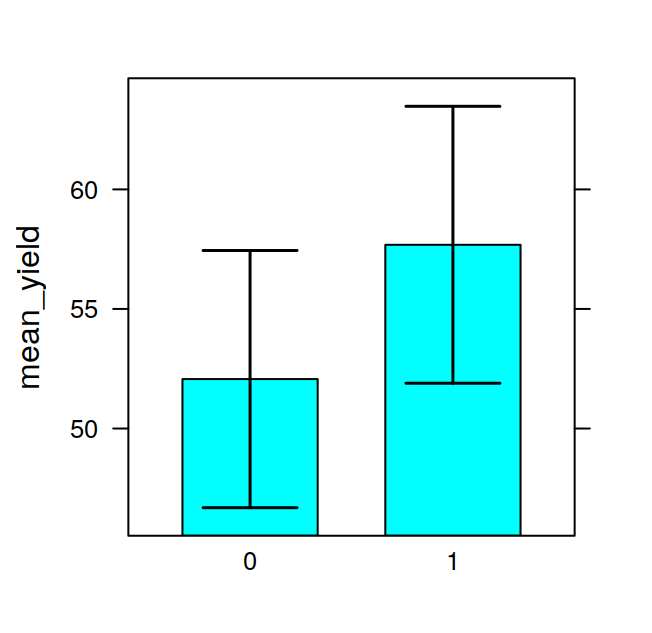

Figure 9.9: Barchart with error bar with no multipanel conditioning and no groups.

we first source the barchart_errbar.R file containing the custom panel and prepanel functions needed to draw the barchart with error bars, and then call the barchart function to draw the plot. Compared to a normal barchart we need to pass it a few additional arguments: the ci.l and ci.u vectors representing the lower and upper error bars limits; plot.ci, a boolean indicating whether to draw the error bars or not; prepanel, which is used to pass the prepanel.barchart_errbar function that sets the y axis limits so as to accommodate the error bars; a custom panel function, which in turn calls the panel.barchart_errbar function. Both prepanel.barchart_errbar, panel.barchart_errbar are functions defined in the barchart_errbar.R file. The resulting plot is shown in Figure 9.9

Next we’re going to look at the case of a single panel with a groups argument. For the next example we generate a new summary dataset as a function of N and P:

npk_summ_NP = npk %>% group_by(N,P) %>% summarize(mean_yield=mean(yield),
                                                  sd_yield=sd(yield))
npk_summ_NP$ci.l = npk_summ_NP$mean_yield - npk_summ_NP$sd_yield
npk_summ_NP$ci.u = npk_summ_NP$mean_yield + npk_summ_NP$sd_yield

then we draw the barchart (shown in Figure 9.10) with the code below:

p2 = barchart(mean_yield~N, groups=P, data=npk_summ_NP,
              ci.l=npk_summ_NP$ci.l, ci.u=npk_summ_NP$ci.u,
              plot.ci=T, auto.key=list(space="top", points=F, rectangles=T),
              panel=function(x, y, ci.l, ci.u, subscripts,...){
                  ci.l = ci.l[subscripts]
                  ci.u = ci.u[subscripts]
                  panel.barchart_errbar(x,y, ci.l=ci.l, ci.u=ci.u,
                                  subscripts=subscripts,...)
              }, prepanel=prepanel.barchart_errbar
              )
print(p2)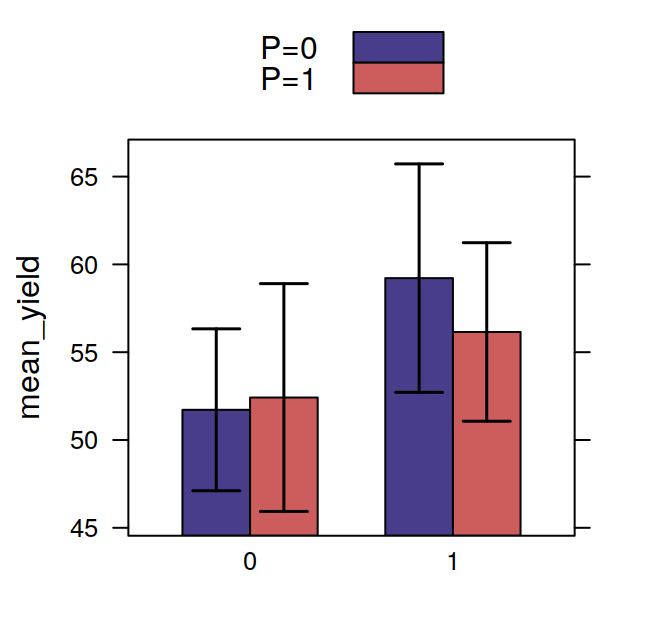

Figure 9.10: Barchart with error bar with groups but no multipanel conditioning.

Finally, we look at the case of multiple panels with grouped bars. For this example we generate a summary dataset as a function of N, P, and K:

npk_summ_NPK = npk %>% group_by(N,P,K) %>% summarize(mean_yield=mean(yield),
                                                     sd_yield=sd(yield))
npk_summ_NPK$ci.l = npk_summ_NPK$mean_yield - npk_summ_NPK$sd_yield
npk_summ_NPK$ci.u = npk_summ_NPK$mean_yield + npk_summ_NPK$sd_yield

then we draw the barchart (shown in Figure 9.11) with the code below:

p3 = barchart(mean_yield~N | P, groups=K, data=npk_summ_NPK,
             ci.l=npk_summ_NPK$ci.l, ci.u=npk_summ_NPK$ci.u,
             plot.ci=T, auto.key=list(space="top", points=F, rectangles=T),
             panel=function(x, y, ci.l, ci.u, subscripts,...){
                      ci.l = ci.l[subscripts]
                      ci.u = ci.u[subscripts]
                      panel.barchart_errbar(x,y, ci.l=ci.l, ci.u=ci.u,
                                      subscripts=subscripts,...)
             }, prepanel=prepanel.barchart_errbar)
print(p3)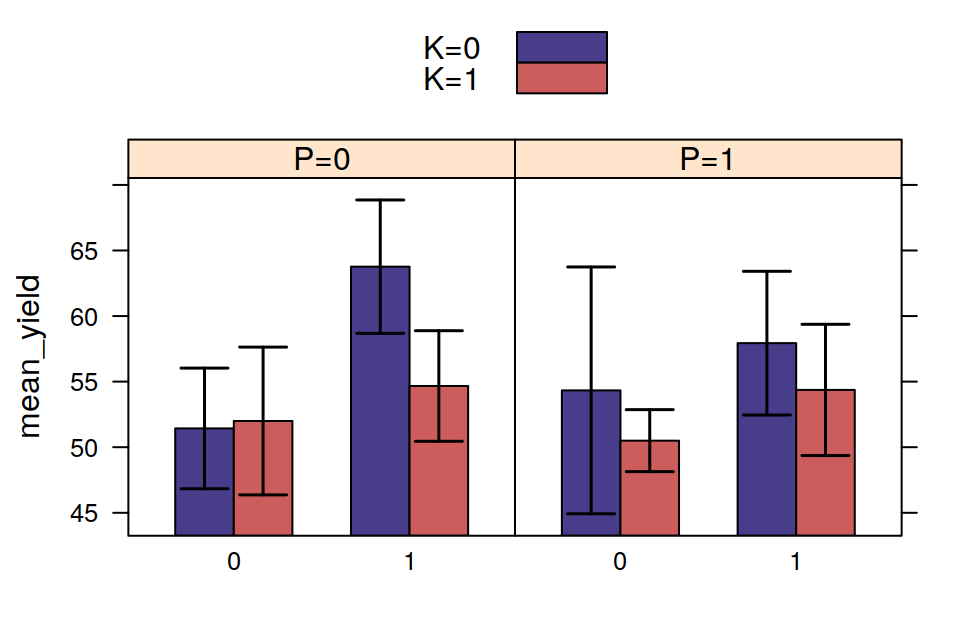

Figure 9.11: Barchart with error bar with groups and multipanel conditioning.

9.3.4 Histograms and density plots

We’ll plot an histogram of sepal length from the iris dataset (Figure 9.12):

data(iris)
p = histogram(~Sepal.Length, data=iris)
print(p)

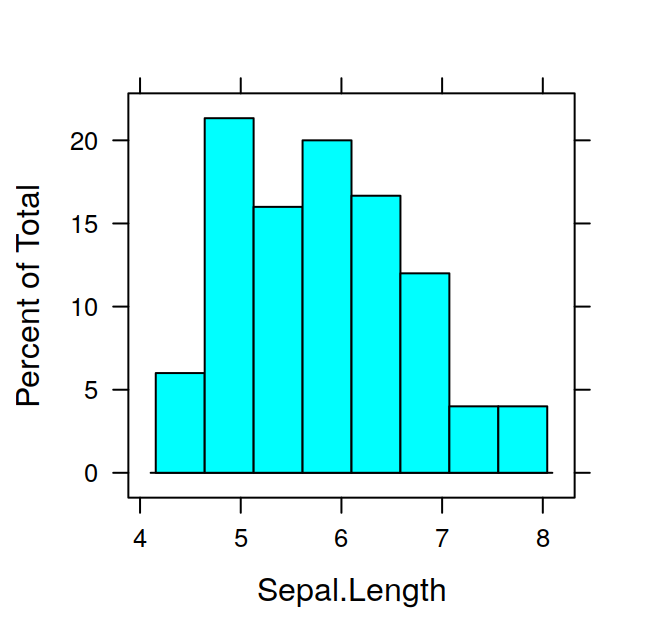
Figure 9.12: Histogram of sepal length in the iris dataset.

the model formula for the histogram function is somehow unusual because the “y” variable is computed by lattice, and we pass the variable for which we want to compute it after the tilde (~). As usual it is also possible to use multi-panel conditioning, as shown by the graph in Figure 9.13, which plots histograms for sepal length separately for each iris species, and was obtained with the code below:

p = histogram(~Sepal.Length | Species, data=iris)
print(p)

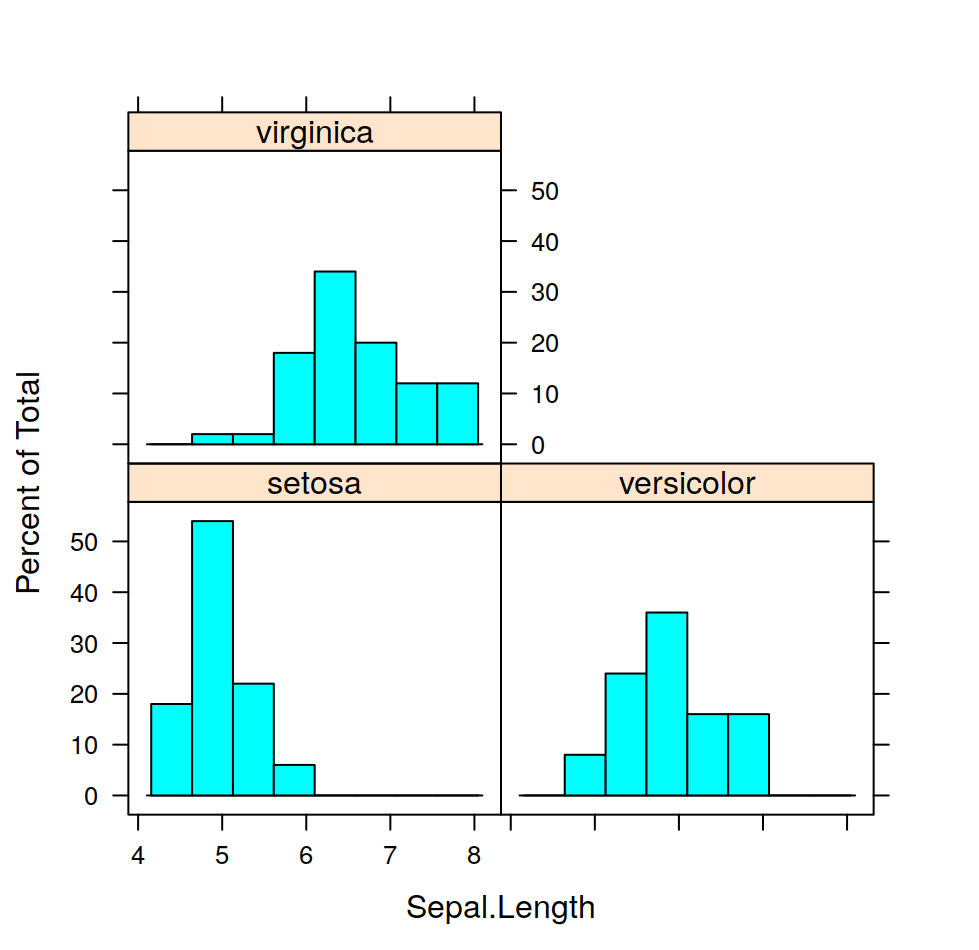
Figure 9.13: Histogram of sepal length in the iris dataset as a function of iris species.

Density plots can be obtained with a similar formula (Figure 9.14):

p = densityplot(~Sepal.Length, data=iris)
print(p)

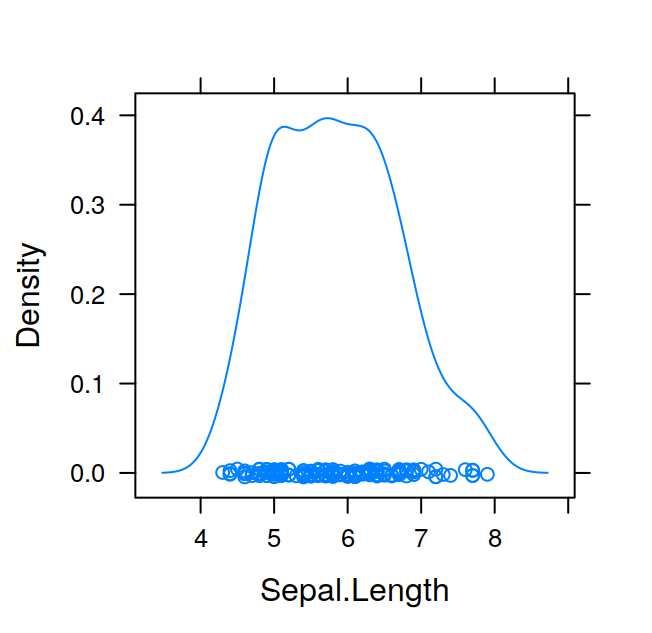
Figure 9.14: Density plot of sepal length in the iris dataset.

by default densityplot plots the individual observation as points. This can be turned off by setting plot.points=FALSE:

p = densityplot(~Sepal.Length, plot.points=FALSE,
                data=iris)

9.3.5 Interaction plots

data(ToothGrowth)
head(ToothGrowth)

##    len supp dose
## 1  4.2   VC  0.5
## 2 11.5   VC  0.5
## 3  7.3   VC  0.5
## 4  5.8   VC  0.5
## 5  6.4   VC  0.5
## 6 10.0   VC  0.5

we’ll first generate a summary dataset as a function of delivery method (supp variable), and dose:

ToothGrowthSumm = ToothGrowth %>% group_by(supp, dose) %>%
                                  summarize(meanLen=mean(len))
ToothGrowthSumm$dose = factor(ToothGrowthSumm$dose)

now we can generate the plot (shown in Figure 9.15) with the following code:

p = xyplot(meanLen~supp, groups=dose, data=ToothGrowthSumm,
           panel="panel.superpose", panel.groups="panel.linejoin",
           auto.key=list(points=F, lines=T, title="Dose", space="right"),
           xlab="Delivery method", ylab="Mean growth")
print(p)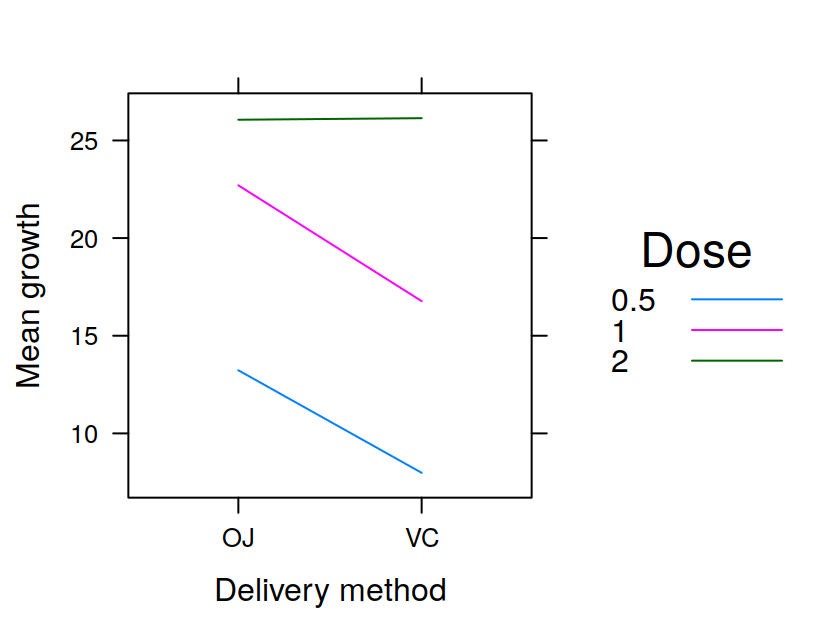

Figure 9.15: Tooth growth by vitamin C dose and delivery method in guinea pigs.

Obtaining an interaction plot with both lines and points requires writing a custon panel function:

panelint = function(x, y, ...){
    panel.points(x, y, ...)
    panel.linejoin(x, y, ...)
}

the plot, shown in Figure 9.16, can then be obtained by using this custom function:

p = xyplot(meanLen~supp, groups=dose, data=ToothGrowthSumm,
           panel="panel.superpose", panel.groups="panelint",
           auto.key=list(points=T, lines=T, title="Dose", space="right"),
           xlab="Delivery method", ylab="Mean growth")
print(p)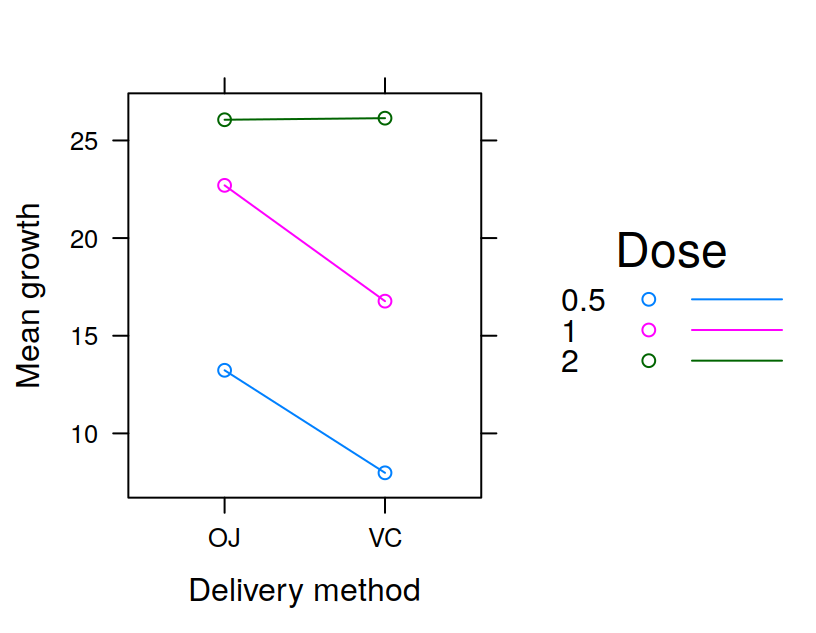

Figure 9.16: Tooth growth by vitamin C dose and delivery method in guinea pigs.

9.4 Customizing lattice graphics

9.4.1 Themes

The function show.settings gives a graphical overview of the current theme. The settings for the current theme are stored in a list, which you can get with:

curr_theme = trellis.par.get()

the list contains many items, which are themselved lists of more basic attributes, we’ll take a peak at the names of the itmes:

names(curr_theme)

we can modify this list, for example setting filled points instead of hollow circles as plot.symbol and superpose.symbol

curr_theme$plot.symbol$pch = 16
curr_theme$superpose.symbol$pch = rep(16, 7)

once this is done we have to call the trellis.par.set function to use the modified list as the current theme:

trellis.par.set(curr_theme)

9.4.2 Textual elements

9.4.2.1 Strip labels

The labels of the panels strips are the names of the levels of the conditioning factor variable. To change their labels you can pass the factor.levels argument to the strip.custom function:

x = rnorm(20)
y = rnorm(20)
treat = factor(rep(c("A", "B"), each=10))
xyplot(y~x|treat, strip=strip.custom(factor.levels=c("Group A", "Group B")))

Figure 9.17: Custom strip labels.

Alternatively, you change the names for the factor levels:

levels(treat) = c("Group A", "Group B")

if you have more than one conditioning factor you can customize the strip labels for each by passing a custom strip function. which.given specifies the conditioning variable that the strip corresponds to:

cnd = factor(rep(c("I", "II"), 10))

customstrip = function(which.given, ..., factor.levels){
    levs = if (which.given==1){
        c("Group A", "Group B")
    } else if  (which.given==2){
        c("Cnd. I", "Cnd. II")
    }
    strip.default(which.given, ..., factor.levels = levs)
}
xyplot(y~x | treat + cnd, strip=customstrip, as.table=TRUE)

Figure 9.18: Custom strip labels with two conditioning factors.

9.4.3 Strips

9.4.3.1 Changing the strip background color

data(iris)
ir2 = iris[iris$Species!="virginica",]
xyplot(Sepal.Length~Sepal.Width | Species, data=ir2, as.table=T,
       par.settings=list(strip.background=list(col="gray90")))

Figure 9.19: Changing strip background color.

or to set a color for several plots:

trellis.par.set(strip.background=list(col="gray90"))

9.4.3.2 Remove “box” and strip borders

The code below plots a figure without a bounding frame and without a strip, the result is shown in Figure 9.20.

axis.L =  function(side, ..., line.col){
    if (side %in% c("bottom", "left")) {
        col = trellis.par.get("axis.text")$col
        axis.default(side, ..., line.col = col)
        if (side == "bottom")
            grid::grid.lines(y = 0)
        if (side == "left")
            grid::grid.lines(x = 0)
    }
}
xyplot(Sepal.Length~Sepal.Width | Species, data=ir2, axis=axis.L,
       scales=list(x=list(alternating=c(1,1)),
                   y=list(limits=c(min(ir2$Sepal.Length),
                                   max(ir2$Sepal.Length)),
                          relation="free")),
       par.settings=list(strip.border=list(col="transparent"),
                         strip.background=list(col="transparent"),
                         axis.line=list(col="transparent")))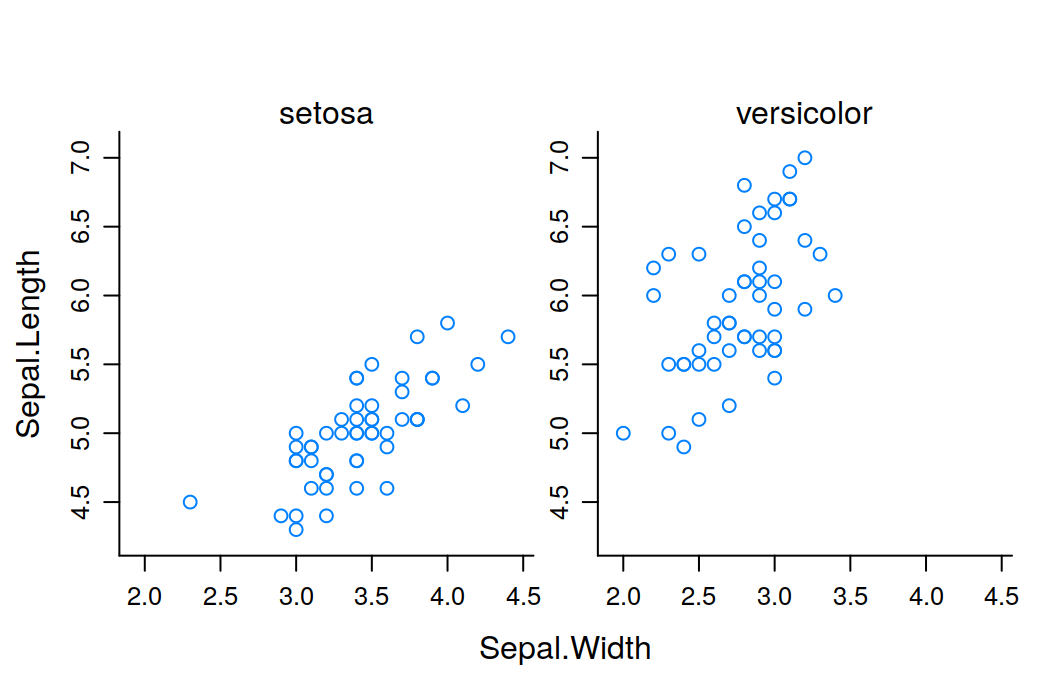

Figure 9.20: Remove strip and box around the panels.

The following code is a variant without tick labels on the inner y panel, the result is shown in Figure 9.21.

axis.L2 =  function(side, ..., line.col){
    if (side %in% c("bottom", "left")) {
        col = trellis.par.get("axis.text")$col
        if (side == "bottom"){
            grid::grid.lines(y = 0)
            axis.default(side, ..., line.col = col, labels="yes")
        }
        if (side == "left"){
            grid::grid.lines(x = 0)
            drawTickLabels = ifelse(current.column() == 1, "yes", "no")
            axis.default(side, ..., line.col = col, labels=drawTickLabels)
        }
    }
}


p = xyplot(Sepal.Length~Sepal.Width | Species, data=ir2, axis=axis.L2, as.table=T,
           scales=list(x=list(alternating=FALSE),
                       y=list(limits=c(min(ir2$Sepal.Length),
                                       max(ir2$Sepal.Length)),
                              relation="free",
                              alternating=4)),
           par.settings=list(strip.border=list(col="transparent"),
                             strip.background=list(col="transparent"),
                             axis.line=list(col="transparent")))
print(p)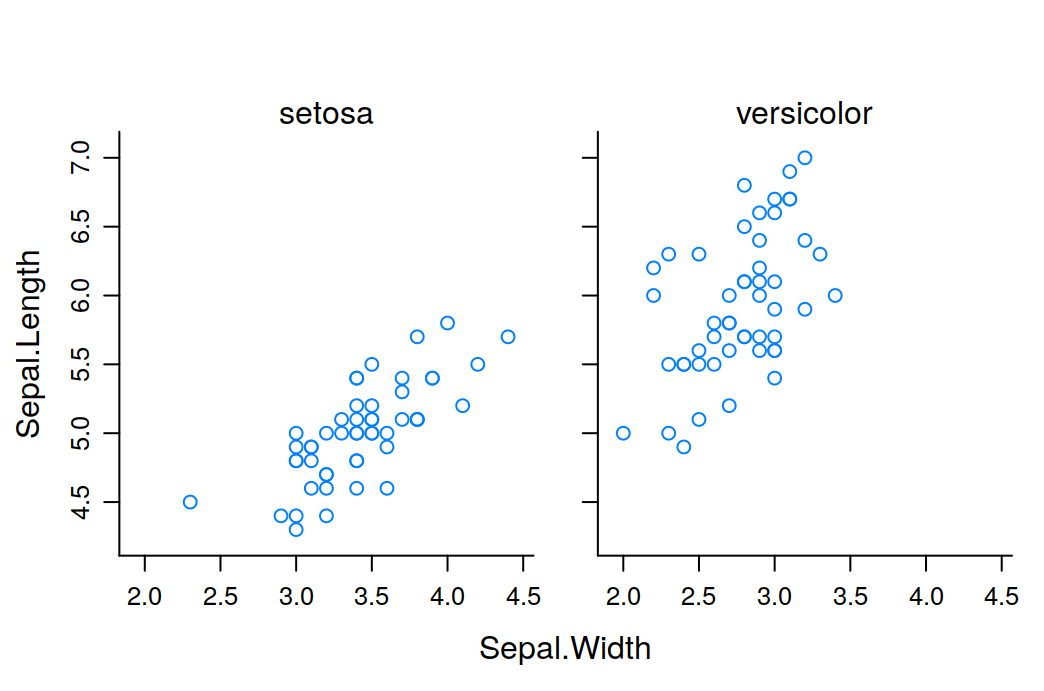

Figure 9.21: Remove strip and box around the panels. Do not draw tick labels on the inner y panel.

9.4.4 Log axis with pretty tickmarks

The latticeExtra package provides a function to get a log axis with pretty tickmarks in lattice, as shown in the code below. The result is shown in Figure 9.22.

library(latticeExtra)
x = as.factor(c("cnd1", "cnd2"))
y = c(0.4, 80)
dat = data.frame(x=x, y=y)
xyplot(y~x, data=dat,
       scales=list(y=list(log=10)),
       yscale.components = yscale.components.log10ticks)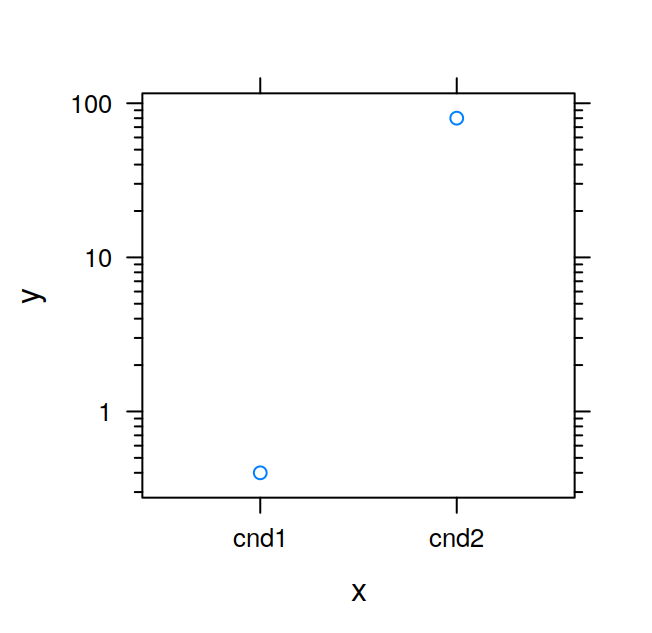

Figure 9.22: Log axis with pretty tickmarks using latticeExtra.

9.4.4.1 Doing it manually

I had written this before discovering the yscale.components.log10ticks function in latticeExtra. I’m leaving it here in case it’s useful for other similar axis customizations.

The procedure to get a log axis with pretty tickmarks manually in lattice is a bit involved. We’ll only cover the log base 10 case here. The first step is to define a function that returns the tick locations:

log10Ticks = function(lim, onlyMajor=FALSE){
    minPow = floor(log10(lim[1]))
    maxPow = ceiling(log10(lim[2]))
    powSeq = seq(minPow, maxPow)
    majTicks = 10^powSeq
    minTicks = numeric()
    for (i in 1:length(majTicks)){
        bb = (1:10)/10;
        minTicks = c(minTicks, (bb*10^powSeq[i]))
    }
    if (onlyMajor==TRUE){
        axSeq = majTicks
    } else {
        axSeq = minTicks
    }
    axSeq = axSeq[lim[1] <= axSeq & axSeq <= lim[2]]
    return(axSeq)
}

by default the function returns both the major (e.g. 1, 10, 100, etc…) and the minor (e.g. 2, 3, 4,…20, 30, 40, etc…) tick locations, but returns only the major tick locations if onlyMajor=TRUE. This function will be used by the yscale.components.log10 function below. This function will be passed as the yscale.components argument in the xyplot call that generates the graph. The yscale.components.log10 function will return a list specifying all parameters of the y axis. To simplify this process the function calls the yscale.components.default function to retrieve the default parameters, and then simply modifies some of these parameters to draw the pretty log axis:

#the function is automatically passed the limits of the panel as an argument
yscale.components.log10 = function(lim, ...){
    #retrieve default parameters
    ans = yscale.components.default(lim = lim, ...)
    #compute major and minor tick locations
    tick.at = log10Ticks(10^lim, onlyMajor=FALSE)
    #compute major tick locations only
    tick.at.major = log10Ticks(10^lim, onlyMajor=TRUE)
    #which are the major ticks?
    major = tick.at %in% tick.at.major
    #where the ticks should be position
    ans$left$ticks$at = log10(tick.at)
    #set tick length, depending on whether minor or major
    ans$left$ticks$tck = ifelse(major, 1.5, 0.75)
    #labels location
    ans$left$labels$at = log10(tick.at)
    #set tick labels
    ans$left$labels$labels = as.character(tick.at)
    #set minor tick labels as empty
    ans$left$labels$labels[!major] = "" 
    ans$left$labels$check.overlap = FALSE
    return(ans)
}

once the yscale.components.log10 function is ready, we can use it in the call to xyplot, note that we also need to set the y scale to log10 in the scales argument, as shown in the code below. The result is shown in Figure 9.23.

x = as.factor(c("cnd1", "cnd2"))
y = c(0.4, 80)
dat = data.frame(x=x, y=y)
xyplot(y~x, data=dat,
       scales=list(y=list(log=10)),
       yscale.components = yscale.components.log10)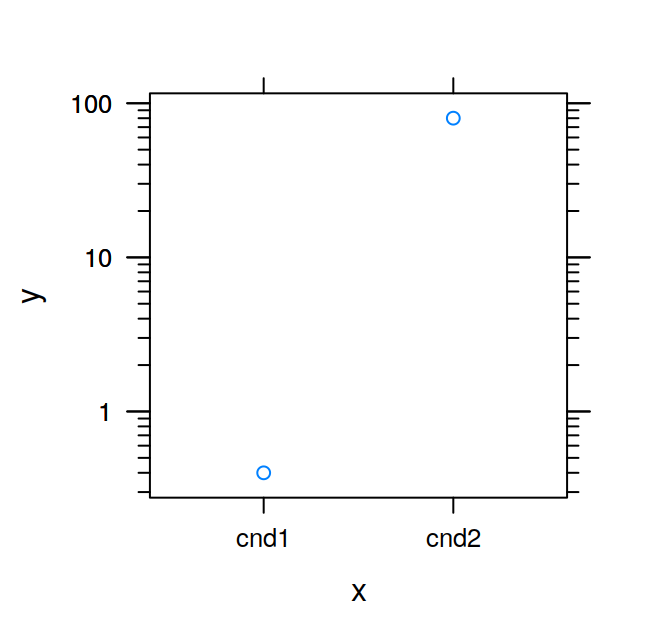

Figure 9.23: Log axis with pretty tickmarks.

9.4.5 Adding regression lines/curves to a `xyplot`

For this example we’ll use the mpg dataset from the ggplot2 package:

mpg = ggplot2::mpg

A loess can be easily added by passing a type argument to xyplot:

xyplot(hwy~displ|drv, data=mpg, type=c("p", "smooth"), as.table=T)

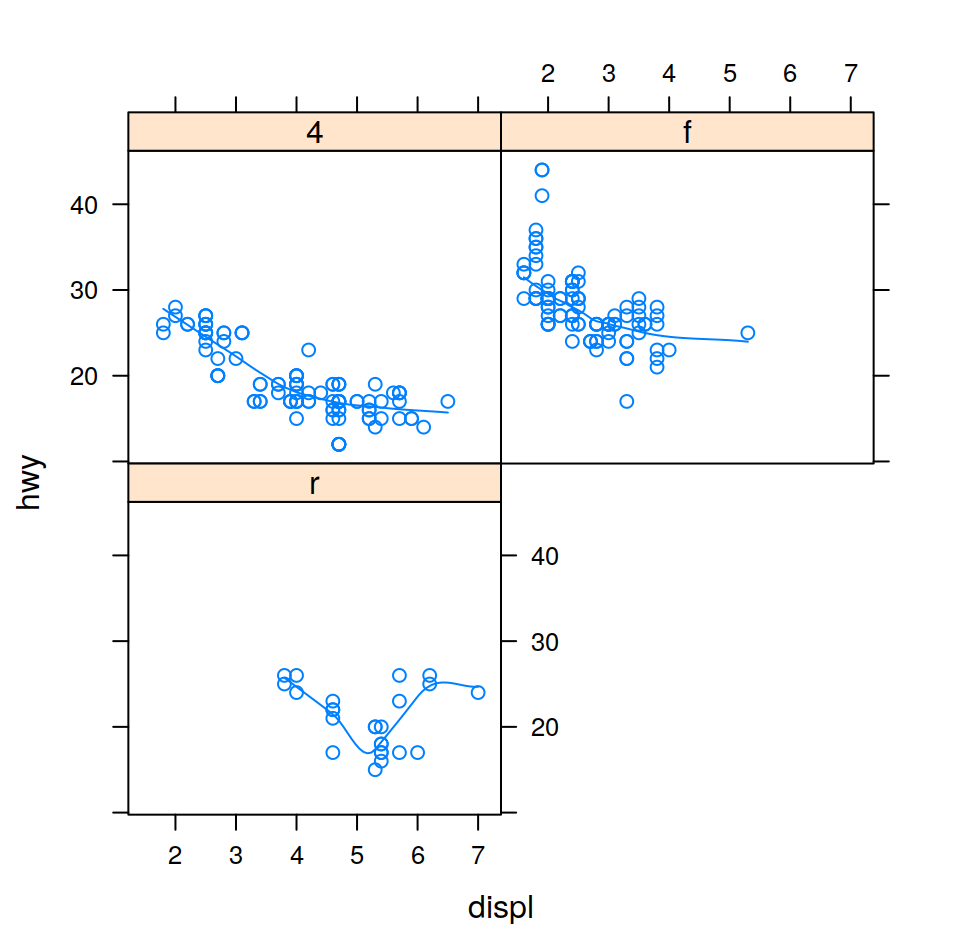
Figure 9.24: xyplot with a loess curve.

in this case we passed a vector with elements p, for the points, and smooth for the loess curve. The resulting plot is shown in Figure 9.24.

A linear fit line can be added by passing r as an element in the type argument vector, as shown in the next example using the iris dataset (plot shown in Figure 9.25):

data(iris)
xyplot(Sepal.Length~Petal.Length|Species, data=iris,
       type=c("p", "r"), as.table=T)

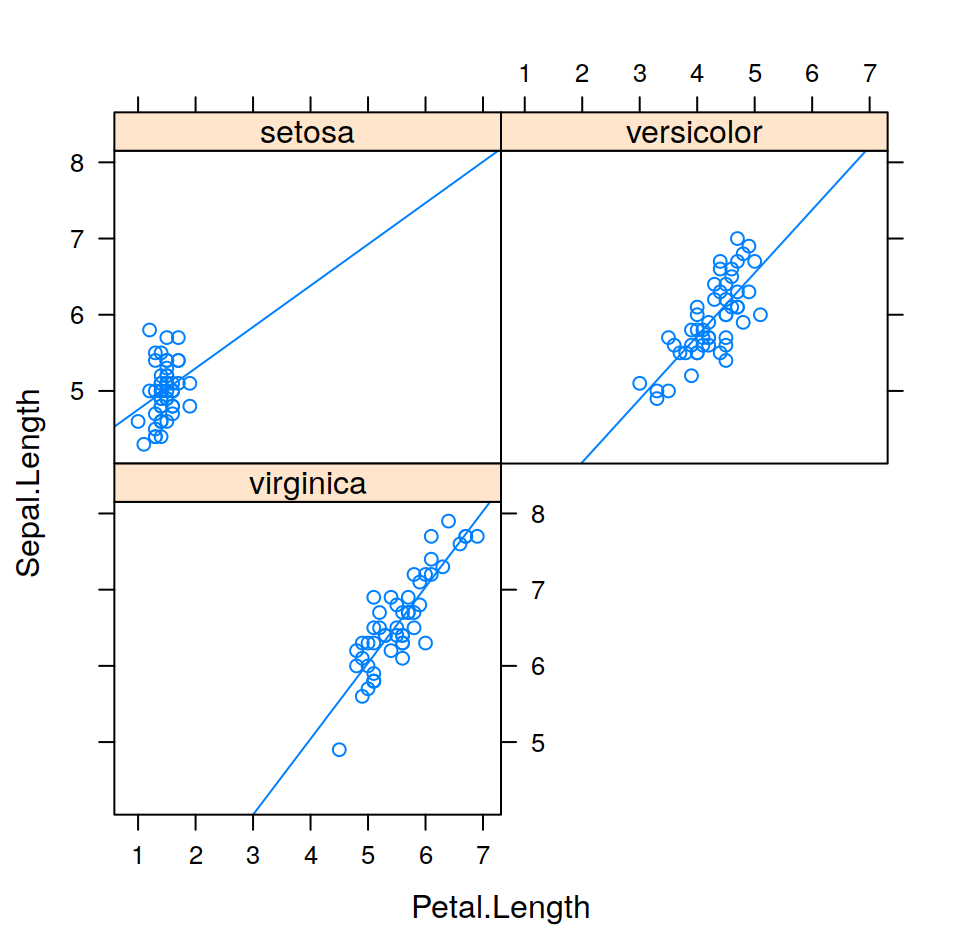
Figure 9.25: xyplot with a linear fit line.

The panel.smoother function in the latticeExtra package can additionally plot confidence bands.

9.5 Writing panel functions

Panel functions allow to customize and extend lattice plots, and can be used to generate new types of plots. The underlying system is sophisticated, but also complex, and overall writing panel function is not easy. Your mileage may vary, some simple customizations and extensions may be relatively easy, but it may be tricky to customize complex plots that include both conditioning and grouping variables. I am still far from mastering the system for writing panel functions, and these notes simply reflect what I’ve learnt so far.

9.5.1 Combining panel functions

Rather than writing a new panel function from scratch, often you just want to add some elements to a plot, for example a regression line, or error bars. The easiest way to do this is writing a panel function that combines two standard panel functions. There are a number of predefined panel functions (see ?panel.functions) that can be used to add lines, grids etc…, to a scatterplot, barchart or other high-level lattice plotting function.

We’ll start with a very simple example: adding a horizontal line at a fixed height in each panel. The dataset below contains a variable y with both positive and negative values:

dat = data.frame(y=c(-0.5, 0.7, 1, -0.8, -0.75, 0.25, 0.32, -0.1),
                 fct1=rep(rep(c("A", "B"), each=2), 2),
                 fct2 = rep(c("L1", "L2"), 4),
                 fct3 = rep(c("F1", "F2"), each=4)
                 )

we can visualize it with a dotplot (Figure 9.26):

trellis.par.set(superpose.symbol = 
                list(col = c("darkslateblue", 
                "indianred"), pch=19))
p1 = dotplot(y ~ fct1 | fct2, groups=fct3, 
            data=dat, auto.key=TRUE, 
            aspect=1, as.table=TRUE)
p1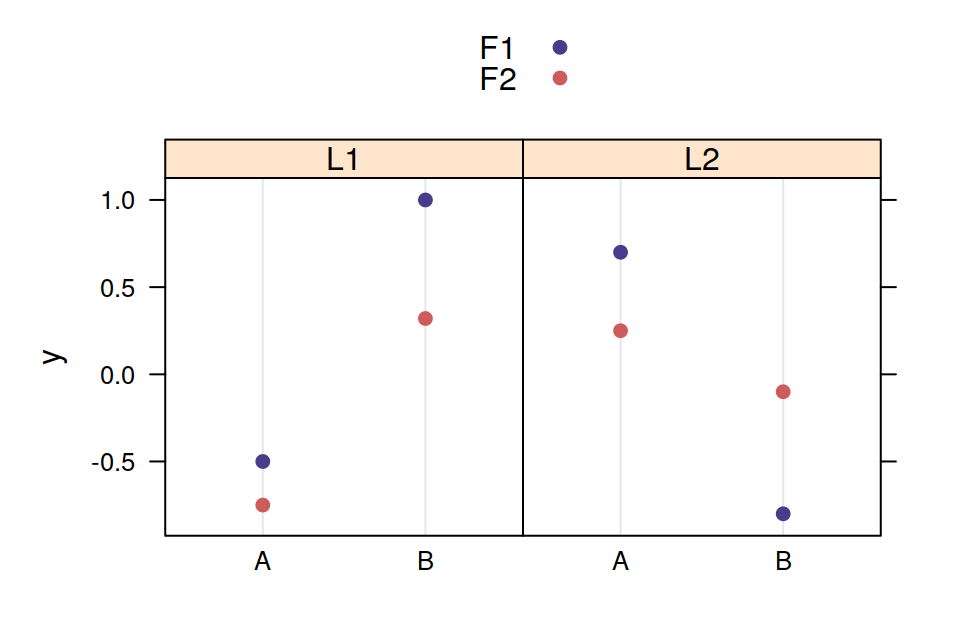

Figure 9.26: Dotplot without a horizontal line at y=0.

however, because the data represent positive or negative displacements from zero, it would be useful to add a horizontal line passing at zero. In order to do this, we’ll write a panel function that combines the panel.dotplot function with the panel.abline function. The latter function will be used to add the horizontal line:

panel.hRefDotplot = function(x, y, ref=NULL, ...){
    panel.dotplot(x, y, ...)
    panel.abline(h=ref, ...)
}

our new panel.hRefDotplot panel function accepts three arguments, x and y, which are “standard” arguments passed by the higher-level plotting functions (like dotplot, or xyplot) to panel functions to specify the data to draw. The third argument represents the position at which to draw the horizontal line of reference for the data; we want it to be zero in this case, but passing the argument as a variable rather than hard-coding the value into the panel function will allow us to recycle this panel function in case we want the horizontal reference line drawn at some other points in the future. Besides these arguments, our panel function accepts also an undefined number of other arguments, which are designated by the ... notation. These are usually graphics parameters that can be specified in the high level plotting function. Our panel.hRefDotplot function is quite simple: we first call panel.dotplot to draw the standard dotplot, and then call panel.abline giving it the value of ref to draw the horizontal line in each panel. The actual plot (Figure 9.27) is done by calling the high level dotplot function and specifying panel.hRefDotplot as the panel function to use:

p2 = dotplot(y ~ fct1 | fct2, groups=fct3, 
            data=dat, auto.key=TRUE, 
            aspect=1, as.table=TRUE,
            panel=panel.hRefDotplot, ref=0)
p2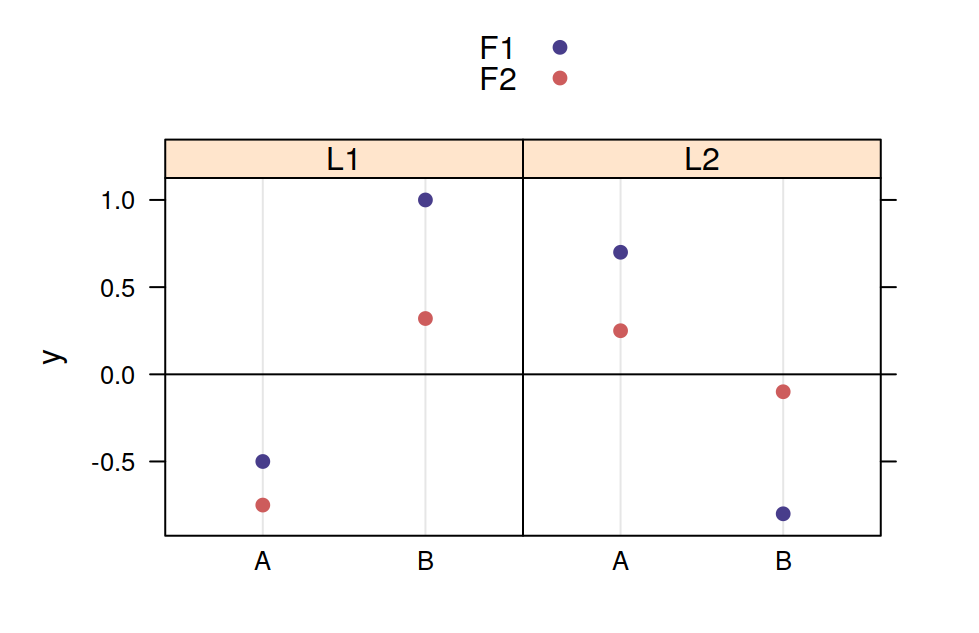

Figure 9.27: Dotplot with a horizontal reference line.

Note the last line of the call: first, we’re telling dotplot to use our hRefDotplot function to do the plotting by specifying the panel argument, second we’re specifying another argument, ref in the call, this is not a standard argument, but it will be automatically passed to our panel function to decide at which height to draw the horizontal line.

9.5.2 Adding error bars to an `xyplot` (single panel, no groups)

We now move on to a slightly more complex example. Adding error bars to an xyplot consisting of a single panel, and with no groups variable. For this example we’ll use the iris dataset, and in particular we’ll plot the mean sepal width $\pm 1$ sd as a function of species. The following lines of code prepare the dataset to plot:

data(iris)
iris_summ = iris %>% group_by(Species) %>%
    summarize(mean_sep_w = mean(Sepal.Width), sd_sep_w=sd(Sepal.Width))
iris_summ$ylow = iris_summ$mean_sep_w - iris_summ$sd_sep_w
iris_summ$yup = iris_summ$mean_sep_w + iris_summ$sd_sep_w

The last two lines of code add a ylow and a yup variable, which represent the lower and upper y coordinates of the error bars. Because error bars take space, we have to increase the limits of the y axis. We could do this “manually” by adding a ylim argument to xyplot a more elegant solution is to pass a prepanel function that computes the limits taking into account the space taken by the error bars:

prepanel.err = function(x, y, ylow, yup, ...){
     list(ylim = range(y, yup, ylow, finite = TRUE)) 
}

Next, we write the panel function that calls xyplot, and adds the error bars by calling panel.arrows:

panel.err0 = function(x, y, ylow, yup,
             col.line=trellis.par.get()[["superpose.line"]][["col"]][1],
                      ...){
             panel.xyplot(x, y, ...)
             panel.arrows(x0 =x, y0 =ylow, x1=x, y1=yup,
                          angle=90, end="both",
                          col=col.line,
                          length=0.1, ...)
}

we can now draw the plot, which is shown in Figure 9.28, with the following code:

p = xyplot(mean_sep_w~Species, data=iris_summ,
           ylow=iris_summ$ylow, yup=iris_summ$yup,
           panel=panel.err0, prepanel=prepanel.err)
p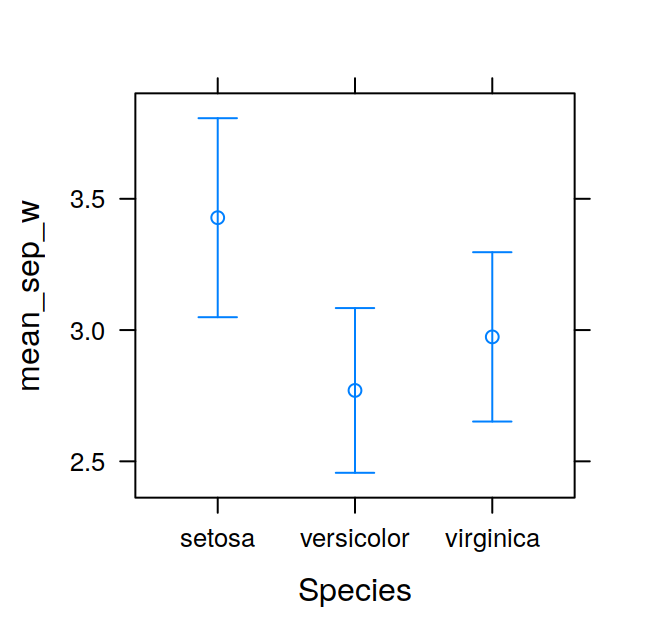

Figure 9.28: xyplot with error bars for a single panel with no groupings.

the only differences from a plain xyplot call is that we’re passing our panel and prepanel functions as additional arguments.

9.5.3 Adding error bars to an `xyplot` with multiple panels (no groups)

We move on to the case of adding error bars to a xyplot with multiple panels, but no groups variable. We’ll use the npk dataset, and in particular we’ll plot the mean yield $\pm 1$ sd as a function of N and P administration. The following lines of code prepare the dataset to plot:

data(npk)
npk_summ_NP = npk %>% group_by(N,P) %>% summarize(mean_yield=mean(yield),
                                                  sd_yield=sd(yield))
npk_summ_NP$ylow = npk_summ_NP$mean_yield - npk_summ_NP$sd_yield
npk_summ_NP$yup = npk_summ_NP$mean_yield + npk_summ_NP$sd_yield

The panel function that we’re going to use is given by the following lines of code:

panel.err1 = function(x, y, subscripts, ylow, yup,
             col.line=trellis.par.get()[["superpose.line"]][["col"]][1],
              ...){
    panel.xyplot(x, y, ...)
    panel.arrows(x0 =x, y0 =ylow[subscripts], x1=x, y1=yup[subscripts],
                 angle=90, end="both",
                 col=col.line,
                 length=0.1, ...)
}

Note how besides the ylow and yup variables the function accepts an additional subscripts variable. This variable holds the indexes of the rows of the dataframe that are used to plot a given panel. The x and y variables have already been “filtered” to contain only the values needed for a given panel; the ylow and yup variables need to be “filtered” using the subscripts. The call to xyplot is given below, and the resulting plot is shown in Figure 9.29:

p = xyplot(mean_yield~N | P, data=npk_summ_NP,
           ylow=npk_summ_NP$ylow, yup=npk_summ_NP$yup,
           panel=panel.err1, prepanel=prepanel.err)
p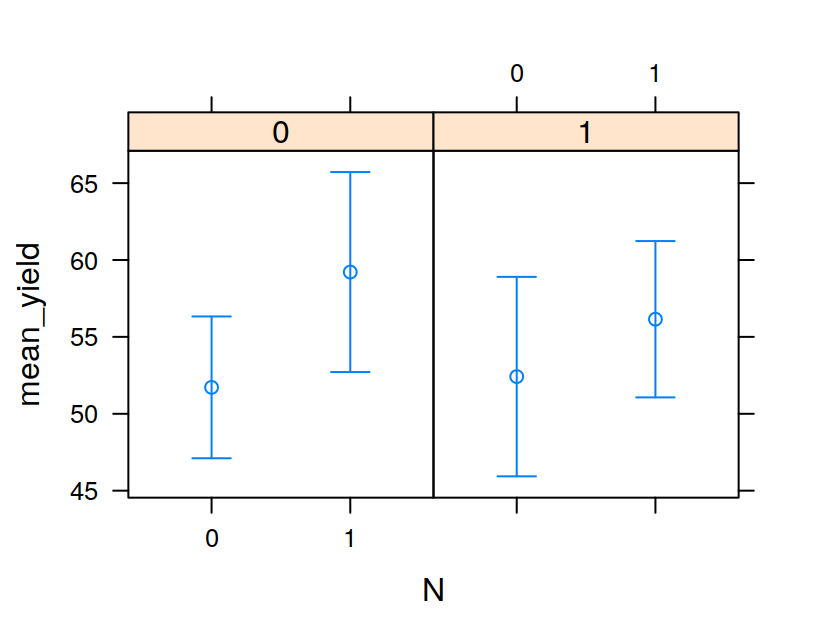

Figure 9.29: xyplot with error bars for a multiple panels with no groups.

we’re reusing the prepanel function from the last example (prepanel.err) because for this plot the computations for the y limits are the same.

9.5.4 Adding error bars to an `xyplot` with groups (single panel)

We’ll now look at the case of adding error bars to an xyplot in a single panel but with a groups variable. We’ll use the same dataset, and the same prepanel function that we employed in the last example. The panel function is given below:

panel.errg = function(x, y, subscripts, ylow, yup, col.line="black", ...){
    panel.xyplot(x, y, ...)
    panel.arrows(x0=x, y0=ylow[subscripts], x1=x, y1=yup[subscripts],
                 end="both", angle=90, col=col.line, length=0.1)
}

in this case subscripts reflects the indexes of the rows of the dataframe containing the values for a given group. The call to xyplot is shown below, and the resulting plot is shown in Figure 9.30:

p = xyplot(mean_yield~N, groups=P, data=npk_summ_NP,
           ylow=npk_summ_NP$ylow, yup=npk_summ_NP$yup,
           panel=panel.superpose, panel.groups=panel.errg,
           prepanel=prepanel.err)
p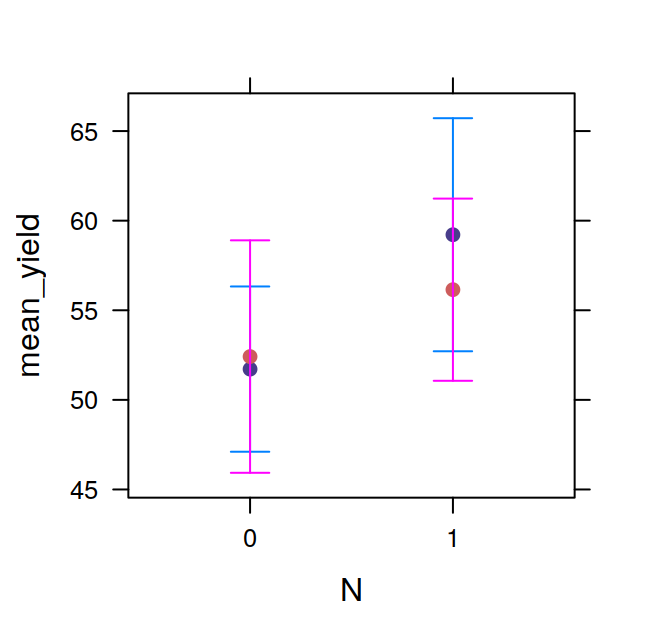

Figure 9.30: xyplot with error bars with groups.

when groups are involved, lattice calls panel.superpose to handle plotting the data of different groups with distinguishing attributes (e.g. colors, line type, etc…). panel.superpose then calls a panel.groups function to handle the actual plotting for each group. In this case we’re passing our custom panel.groups function to add error bars.

We’ve achieved our aim of adding error bars, but there’s an issue: the bars are overlapping and the plot looks ugly. To fix this issue we write another panel function which will slightly offset the position of the points and the bars on the x axis depending on which group is being plotted. To be able to do this, we let the function accept the group.number argument, a number denoting which group is being plotted:

panel.errg2 = function(x, y, subscripts, group.number,
                       ylow, yup, col.line="black", ...){
    offs = ifelse(group.number==1, -0.1, 0.1)
    x = x + offs
    panel.xyplot(x, y, ...)
    panel.arrows(x0=x, y0=ylow[subscripts], x1=x, y1=yup[subscripts],
                 end="both", angle=90, col=col.line, length=0.1)
}

The call to xyplot is shown in the code below, and the resulting plot, which now looks better, is shown in Figure 9.31:

p = xyplot(mean_yield~N, groups=P, data=npk_summ_NP,
           ylow=npk_summ_NP$ylow, yup=npk_summ_NP$yup,
           panel=panel.superpose, panel.groups=panel.errg2,
           prepanel=prepanel.err)
p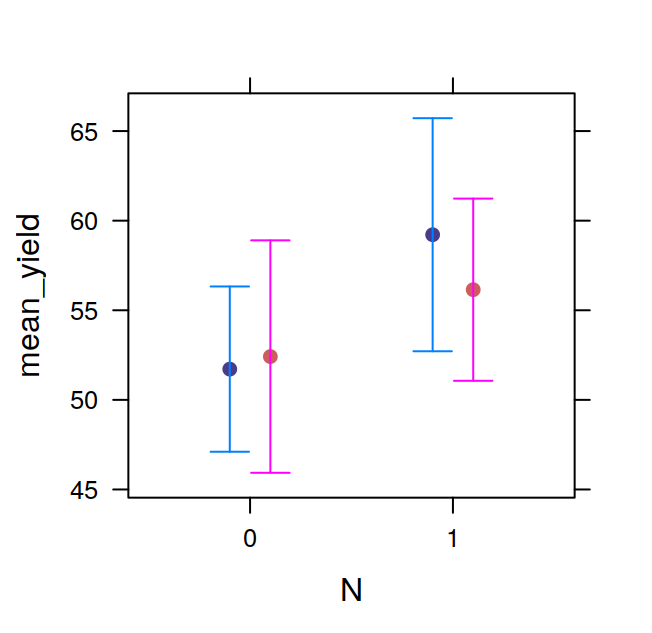

Figure 9.31: xyplot with error bars with groups.

9.5.5 Adding error bars to an `xyplot` with groups and multiple panels

We’ll now move on to the case of adding error bars to an xyplot with multiple panels and a grouping variable. For this example we’ll again use the npk dataset, but this time we’ll plot the mean yield $\pm 1$ sd as a function of N, P, and K administration. The following lines of code prepare the dataset to plot:

npk_summ_NPK = npk %>% group_by(N,P,K) %>% summarize(mean_yield=mean(yield),
                                                     sd_yield=sd(yield))
npk_summ_NPK$ylow = npk_summ_NPK$mean_yield - npk_summ_NPK$sd_yield
npk_summ_NPK$yup = npk_summ_NPK$mean_yield + npk_summ_NPK$sd_yield

We won’t need to write a new prepanel or a new panel function, because those from the last example will be suitable also for the current plot. The call to xyplot is shown in the code below, and the plot is shown in Figure 9.32:

p = xyplot(mean_yield~N | K, groups=P, data=npk_summ_NPK,
           ylow=npk_summ_NPK$ylow, yup=npk_summ_NPK$yup,
           panel=panel.superpose, panel.groups=panel.errg2,
           prepanel=prepanel.err)
p

Figure 9.32: xyplot with error bars with groups and multiple panels

9.6 Further resources

9.6.1 Books, articles, and tutorials

9.6.2 Related packages

latticeExtra provides several additional high-level plotting functions and many utility functions. wzRfun contains miscellaneous utilities, including panel functions to add error bars and error bands to lattice plots.

10 Graphics: common elements across plotting libraries

Although as we have seen R has a number of different plotting libraries, certain plotting procedures, such as choosing colors, choosing fonts, and annotating plots with mathematical expressions that share the same or similar underlying mechanisms/functions across the different plotting libraries. This chapter will illustrate some of these common functions.

10.1 Colors for graphics

The command colors gives a list of built-in colors available for graphics in R. You can see some of these colors in Figure 10.1. There are 101 built-in shades of gray, from gray0, that is almost black, to gray100 that is almost white, you can see some of them in Figure 10.1. A complete table of built-in R colors is given in Appendix D.

Figure 10.1: Some built-in colors in R.

You can also specify colors in rgb values. By default R accepts values in the range 0-1, but you can change the range with the max option to set the range as 0-255. Please note that changing the range doesn’t change the colors you can use, it just changes the values you use to specify them, so for example the following graphs will have the same colors:

vec = c(3,6)
barplot (vec, col= c(rgb(0.176, 0.262, 0.49),
         rgb(0.568, 0.254 0.654)))
barplot (vec, col= c(rgb(45,67,125, max=255),
         rgb(145,65,167, max=255)))

the first uses the default range, and the second uses the range 0-255, but I simply derived the values for the first graph, dividing those for the second by 255.

The function col2rgb can be used to get the rgb values of a built-in color from its name. The rgb values are given in this case in the range 0-255. Here’s an example:

col2rgb("lightslateblue")

##       [,1]
## red    132
## green  112
## blue   255

10.1.1 Color opacity

The adjustcolor function can be used to set the opacity of a color using the alpha.f argument:

mycol = adjustcolor("skyblue", alpha.f=0.5) 
x = rnorm(1000)
y = rnorm(1000)
plot(x, y, pch=21, bg=mycol, cex=1.5)

Figure 10.2: Color opacity.

the adjustcolor function accepts a vector of colors as an argument, so you can change the transparency of several colors at the same time.

10.1.2 Color palettes

The RColorBrewer package provides a number of discrete color palettes. The complete set is shown in Figure 10.3 can be seen with the following function:

library(RColorBrewer) #load package
display.brewer.all()

Figure 10.3: RColorBrewer palettes.

to show only colorblind friendly palettes:

display.brewer.all(colorblindFriendly=T)

the palettes can be instantiated by calling the brewer.pal function as follows:

pal1 = brewer.pal(3, "Pastel2")

the first argument is the number of colors and the second argument is the name of the desired palette. Note that ggplot2 has convenience functions to use RColorBrewer palettes (see here).

The colorspace package provides an array of utilities for working with colors, including color palettes in HCL color space.

The viridis package provides a number of continuous color palettes that have been designed to be perceptually uniform and robust to color blindness (see the viridis vignette). Note that ggplot2 has convenience functions to work with viridis palettes (see here).

It is important to make sure that important graphical features distinguished by colors can be seen by everyone, including colorblind people. The dichromat package can simulate the effects of different types of color blindness through the dichromat function. The colorspace package can also simulate color vision deficiencies through the simulate_cvd function.

Another useful colorblind friendly palette is that provided by Okabe and Ito here; you can instantiate this palette with the following code:

cbPalette = c("#000000", "#E69F00", "#56B4E9", "#009E73", "#F0E442",
              "#0072B2", "#D55E00", "#CC79A7", "#999999")

10.2 Mathematical expressions and variables

It is possible to use mathematical symbols in plot labels and text. The base system for providing math symbols in plot annotations has been described by Murrell and Ihaka (2000), which is a recommended reading. An overview of the system with a comprehensive list of all the symbols can be obtained with ?plotmath. I don’t find the system particularly intuitive, and can’t claim to fully understand its inner workings, but I’ll nevertheless attempt to explain in rough terms how it works.

The basic idea is that instead of providing a string to text, xlab or other functions through which you want to plot some text, you provide an expression, in the sense of a mathematical expression. Two examples are given below:

plot.new(); plot.window(xlim=c(4, 6), ylim=c(0, 5))
text(5, 1, labels=expression(alpha/(x+2)))
text(5, 2.5, labels=expression(frac(alpha, x+2)))
box()

note how alpha is turned into the corresponding Greek letter. Often you’ll want to combine strings with mathematical expressions in labels. This can be achieved using the paste function, as shown below:

plot.new(); plot.window(xlim=c(4, 6), ylim=c(0, 5))
text(5, 1, labels=expression(paste("Amplitude (", mu, "V)")))
box()

Strings and mathematical expressions can also be combined using the multiplication (*) operator (e.g. expression("Amplitude (" * mu * "V)")), but this seems somewhat improper and runs into limitations. For example expression(alpha == 3 * beta == 2) results in an error, probably because it is not a valid mathematical expression, while expression(paste(alpha == 3, beta == 2)) works without errors.

Spaces between symbols can be obtained by using one or more tilde (~) operators, as shown below:

plot.new(); plot.window(xlim=c(4, 6), ylim=c(0, 5))
text(5, 1, labels=expression(paste("No spaces: ", alpha * beta)))
text(5, 2.5, labels=expression(paste("Spaces: ", alpha ~ beta)))
box()

Sometimes you may want to print the value of a variable inside the expression of a plot label. In this case you can use the substitute function:

x = rnorm(100); y=rnorm(100)
corrOut = cor.test(x,y)
corrEst = corrOut$estimate
corrPVal = corrOut$p.value
plot(x,y)
title(main=substitute(rho == v1, list(v1=round(corrEst,2))))

the second argument to the function is a list of all the variable values that need to be substituted. In the example below two values are substituted:

plot(x,y)
title(main=substitute(paste(rho == v1, "; ", italic(p) == v2),
                      list(v1=round(corrEst,2), v2=round(corrPVal, 2))))

A few more example of mathematical expressions in labels are given below:

uVText = expression(paste("Amplitude (", mu, "V)"))
dF0Text = expression(paste( Delta, 'F0 (%)'))
dpText = expression(paste(italic("d' ")))
subText1 = expression(paste(sigma, scriptscriptstyle(c), " (Cents)"))
subText2 = expression(paste(delta, scriptscriptstyle(k)  %+-% 162.5,
                            ' Cents', sep=''))
sqText = expression(paste('F0 Acceleration (Hz/', s^2, ')'))
piText = expression(paste('Start Phase 1.5', pi,))
betaText = expression(beta[0])
log10Text = expression(log[10](nu))
uVsqText = expression(paste('Level ', italic('re'), ' 1 ',
                            mu, V^{2}, ' (dB)'))
bdText = expression(paste( bold("Enhancement ("),
                          italic("d'"), bold("units)")))
zScoreText = expression(paste(italic(z), " Score"))
densText = expression(paste("Density (", kg/m^3, ")"))
beta2Text = expression(mu[beta[0]])
noiseText = expression(paste("Noise [", log[10], "(Energy)]"))
PTAText = expression(paste("PTA"["0.5-2"], " (dB)"))
RSqText = expression("R"^"2")
atopText = expression(atop("PTA"["1-2"],"(dB SPL)"))
latencyText = expression(paste("Latency (", italic(z),
                               " Score)"))

par(mfrow=c(2,2))

plot.new(); plot.window(xlim=c(0, 10), ylim=c(0, 10))
text(5, 1.00, labels=uVText)
text(5, 2.25, dF0Text)
text(5, 3.50, dpText)
text(5, 4.75, subText1)
text(5, 6.00, subText2)
text(5, 7.25, sqText)
text(5, 8.5, piText)
text(5, 9.75, betaText)
box()

plot.new(); plot.window(xlim=c(0, 10), ylim=c(0, 10))
text(5, 1.00, labels=log10Text)
text(5, 2.25, uVsqText)
text(5, 3.50, bdText)
text(5, 4.75, zScoreText)
text(5, 6.00, densText)
text(5, 7.25, beta2Text)
text(5, 8.5, noiseText)
text(5, 9.75, PTAText)
box()

plot.new(); plot.window(xlim=c(0, 10), ylim=c(0, 10))
text(5, 1.00, labels=latencyText)
text(5, 2.25, RSqText)
text(5, 3.50, "")
text(5, 4.75, "")
text(5, 6.00, "")
text(5, 7.25, "")
text(5, 8.5, "")
text(5, 9.75, "")
box()
title(xlab=atopText)

10.3 Fonts for graphics

In Section 6.5.4 it was mentioned that it is possible to specify a system font (such as Palatino, or Arial) for the R base graphics via the par(family=...) setting, but this may or may not work depending on the specific graphics device (and of course also on whether that font is installed in your system or not).

I’ll focus on the issue of generating pdfs with custom fonts because I mostly use pdf for saving R graphics. The pdf device does not automaticaly embed the fonts in the file, and works only with a limited number of fonts (see ?pdfFonts for details). An easy way to get around this issues is to use the cairo_pdf device instead of the pdf device: the cairo_pdf device can access all the true type fonts (TTF) and open type fonts (OTF) in your system and also embeds them in the pdf. The device can be used with both base graphics:

cairo_pdf("base_graphics_ubuntu_font.pdf", family="Ubuntu")
plot(1:10)
dev.off()

or with ggplot2, by setting the device argument in ggsave to cairo_pdf:

library(ggplot2)
n=100
dat=data.frame(x=rnorm(n), y=rnorm(n))
p = ggplot(dat, aes(x=x, y=y)) + geom_point()
p = p + xlab("X-Label") + ylab("Y-Label")
p = p + theme(text=element_text(size=12, family="Ubuntu"))
ggsave("ggplot2_cairo_pdf.pdf", p, width=3.4, height=3.4,
       device=cairo_pdf)

An alternative solution for using system fonts in pdfs is the extrafont package. Another alternative is the showtext package. Compared to extrafont the showtext package has the advantage of being able to use open type fonts; however showtext has the disadvantage of not rendering the fonts as “drawings” (you can’t copy and paste text). Overall, my favorite solution is to use cairo_pdf because it handles both TTF and OTF fonts.

11 Preparing graphics for publications

Academic journals usually have a number of stylistic requirements for figures, including for example font family and size, absence of decorative elements such as borders around the figure, and labeling of figures with letters in multi-panel figures. Some people first produce a figure in R (or other software), and then post-process it “manually” using graphics editing software to meet the journal requirements. While this is a viable option, I find it very inefficient and prefer to obtain publication-quality figures directly in R.

11.1 Figure size and fonts

This section will cover some common requirements regarding fonts and print size for publication-quality figures, and applies for figures generated with any of the R graphics systems (R base, ggplot, and lattice). The next sections will present specific examples with each graphics system.

Statistical plots for print journals should be saved in a vector graphics format such as pdf or eps, while images should be saved in a raster graphics format such as tiff.

Academic journals typically require using a sans-serif font with a 12 point size for figure annotations. Use of fonts for R graphics was covered in Section 10.3, but we’ll present some examples in the next sections.

Most journals require you to submit figure files with embedded fonts. For pdf files, the easiest way to do this is to use the cairo_pdf function instead of the pdf function for base R and lattice graphics, and use the device=cairo_pdf in ggsave for ggplot2 graphics; the pdf files saved in this way will have their fonts embedded (see Section 10.3). Alternatively, you can embed fonts using an external program. On Linux I use the following bash script to embed fonts through the gs program:

#! /bin/bash

#usage embed_pdf_fonts input output
gs -q -dNOPAUSE -dBATCH -dEPSCrop \
   -sDEVICE=pdfwrite -dPDFSETTINGS=/prepress \
   -dPrinted=false -sOutputFile=$2 $1

Many academic journals use a two column layout, and have guidelines indicating the maximal physical size of a figure. A figure typically spans either one or two columns, although sometimes also figures spanning one and a half, or only half a column are allowed. The exact requirements re maximum figure width by figure type (1-col, 2-col, etc…) vary from journal to journal, but they are usually close to those indicated in Table 11.1.

Table 11.1: Typical figure width in academic journals for different figure types. Width in given in inches (in), and millimeters (mm).
Fig. type	Fig. width
1/2 column	1.535 in (39 mm)
1 column	3.307 in (84 mm)
1.5 columns	5.078 in (129 mm)
2 columns	6.85 in (174 mm)

The default print size of the figures used by the cairo_pdf and ggsave functions (i.e. if you don’t specify width and height) is much larger than the typical 1-column figure size required by academic journals. It becomes more difficult to fit certain elements (e.g. axis labels) in a smaller space, so it’s best to start saving figures in the smaller size typically required by journals early in the paper write-up process and make sure they look right in that size.

11.1.1 Baser R and `lattice` plots

To obtain pdf figures of a given print width and height we can pass the width and height arguments to the cairo_pdf function, specifying the desired values in inches:

cairo_pdf("Fig1.pdf", width=3.307, height=3.307)

The default font used by cairo_pdf is sans-serif at size 12, so you don’t really need to change that, should you need to you can pass the family and pointsize arguments to the function:

cairo_pdf("Fig1.pdf", width=3.307, height=3.307,
          family="Helvetica", pointsize=12)

11.1.2 `ggplot2`

The pointsize and font depend on the theme you’re using. Many themes use a sans-serif font, so you probably don’t need to change that. However, you may need to change the point size (e.g. the default ggplot2 theme uses an 11 point size). You can change that with theme(text=element_text(size=12)). The following code shows an example of changing both the font family and the point size:

n=100
dat=data.frame(x=rnorm(n), y=rnorm(n))
p = ggplot(dat, aes(x=x, y=y)) + geom_point()
p = p + xlab("X-Label") + ylab("Y-Label")
p = p + theme(text=element_text(size=12, family="Helvetica"))

Alternatively, you can set the font family and pointsize directly when calling a specific theme, as in the following example:

p = p + theme_classic(base_family="Helvetica", base_size=12)

To obtain figures of a certain physical width and height we can pass the width and height arguments to the ggsave function:

ggsave("Fig1.pdf", plot1, width=3.307, height=3.307, device=cairo_pdf)

by default width and height units are in inches, though this can be changed by passing a units argument if desired (see ?ggsave).

11.2 Themes

Many journals require a rather plain style for figures, with a white background, no grid lines, and no “borders” or “boxes” around the figure beside the x and y axes.

11.2.1 Base R

By default plots have a white background and no grid. The “borders” around the figures can be removed through the bty argument. Setting bty to n removes the borders from all sides, while setting it to L leaves the borders around the bottom and left axes:

plot(rnorm(100), bty="L")

11.2.2 `ggplot2`

The theme_classic theme generally follows the style commonly requested by academic journals, so in many cases all you’ll need to do is set this theme, increasing the font point size from 11 to 12:

n=100; dat=data.frame(x=rnorm(n), y=rnorm(n))
p = ggplot(dat, aes(x=x, y=y)) + geom_point()
p = p + xlab("X-Label") + ylab("Y-Label")
p = p + theme_classic(base_size=12)

Alternatively, you can use the theme_cowplot from the cowplot package, which is very similar to theme_classic.

11.2.3 `lattice`

11.3 Multi-panel figures

11.3.1 `ggplot2`

The plot_grid function from the cowplot package can be used to arrange separate ggplot2 plots in a grid layout and label them, as shown in Figure 11.1, which was obtained with the following code:

library(cowplot); library(ggplot2)
data(iris)
p1 = ggplot(iris, aes(Sepal.Width, Sepal.Length)) + geom_point()
p2 = ggplot(iris, aes(Petal.Width, Petal.Length)) + geom_point()
plot_grid(p1, p2, labels = c('A', 'B'), label_size = 12)

Figure 11.1: Multi-panel figure arranged and labeled with the plot_grid function.

11.3.2 `lattice`

The plot_grid function from the cowplot package can be used to arrange separate lattice plots in a grid layout and label them, as shown in Figure 11.2, which was obtained with the following code:

library(lattice)
p1 = xyplot(Sepal.Length~Sepal.Width, data=iris)
p2 = xyplot(Petal.Length~Petal.Width, data=iris)
plot_grid(p1, p2, labels = c('A', 'B'), label_size = 12)

Figure 11.2: Multi-panel figure arranged and labeled with the plot_grid function.

For multi-panel plots obtained via panel conditioning, we can use the page function to add labels. First we write some boilerplate code for preparing the plot.

library(grid)
ir2 = iris[iris$Species!="virginica",]
axis.L =  function(side, ..., line.col){
    if (side %in% c("bottom", "left")) {
        col = trellis.par.get("axis.text")$col
        axis.default(side, ..., line.col = col)
        if (side == "bottom")
            grid::grid.lines(y = 0)
        if (side == "left")
            grid::grid.lines(x = 0)
    }
}

Now we draw the graph (shown in Figure 11.3) with xyplot, and add labels via the page function which uses the whole display area as the default viewport. We use grid functions inside the page function to annotate the plot.

p = xyplot(Sepal.Length~Sepal.Width | Species, data=ir2, axis=axis.L,
           scales=list(x=list(alternating=c(1,1)),
                       y=list(limits=c(min(ir2$Sepal.Length),
                                       max(ir2$Sepal.Length)),
                              relation="free")),
           strip=FALSE,
           par.settings=list(axis.line=list(col="transparent")),
           page = function(n) {
               grid.text(label = "A",
                         x = unit(0.05, "npc"), y = unit(0.96, "npc"),
                         just = c("left", "center"), gp=gpar(fontface=2))
               grid.text(label = "B",
                         x = unit(0.525, "npc"), y = unit(0.96, "npc"),
                         just = c("left", "center"), gp=gpar(fontface=2))
           }
           )
print(p)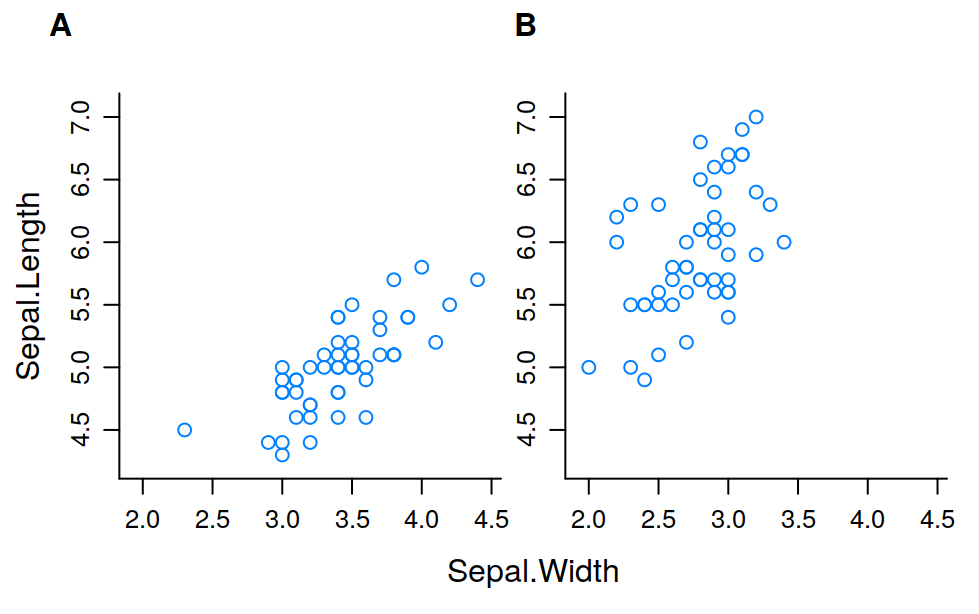

Figure 11.3: lattice panels with labels.

12 Tidyverse

Tidyverse is a collection of R packages that used in conjuction significantly change the way of working with R.

ggplot2 and dplyr are probably the most popular packages in tidyverse. When you start using ggplot2 it becomes almost essential to use dplyr too because ggplot2 is heavily based on dataframes or tibbles as input data. Before covering dplyr we will explain what tibbles are in the next section because dplyr returns tibbles as objects.

12.1 Tibbles

Tibbles are a modern take on dataframes (which we introduced in Section 3.5). Tibbles are in fact very similar to dataframes, but if you’re used to dataframes, there are a few things that may surprise you when you start using tibbles.

Tibbles can be constructed with the tibble function, which is similar to the data.frame function for constructing dataframes:

library(tibble)
dat = tibble(x=rnorm(20), y=rep(c("A", "B"), each=10))

They can be easily converted to dataframes with the as.data.frame function if needed:

dat_frame = as.data.frame(dat)

and dataframes can also be easily converted to tibbles with the as_tibble function:

dat2 = as_tibble(dat_frame)

One feature of tibbles that may surprise you is the fact that, by default, when you use a print method on a tibble only a limited number of rows and columns are shown. This is for me a very annoying thing, because when I load a dataframe I want to see all the columns with the variable names (typically I do this with head(df)). Luckily you can change these defaults by specifying the tibble.print_max and tibble.width options. You can do this in your .Rprofile file in your home directory so that your preference sticks across sessions:

## This goes in .Rprofile in ~/
.First <- function(){
    .libPaths(c((.libPaths()), "~/.R_library/"))
    options(tibble.print_max = Inf)
    options(tibble.width = Inf)
}

Another aspect of tibbles that may surprise dataframe users is their behavior re subsetting. For example, you might expect that the following returns a vector:

dat[dat$y=="A", "x"]

## # A tibble: 10 x 1
##          x
##      <dbl>
##  1  0.0983
##  2 -0.280 
##  3  1.02  
##  4  0.0584
##  5 -0.417 
##  6 -1.74  
##  7  0.365 
##  8 -0.317 
##  9 -1.37  
## 10 -0.501

but it returns a 1-column tibble instead. Furthermore trying as.numeric(dat[dat$y=="A", "x"]) to convert it to a vector doesn’t work. The solution is to use the pull function from dplyr:

library(dplyr)
pull(dat[dat$y=="A", ], x)

##  [1]  0.09831035 -0.27951673  1.02105526  0.05843470 -0.41656644 -1.73980278
##  [7]  0.36467128 -0.31725294 -1.36515908 -0.50087454

More succintly, if, for example, you wanted to run a $t$-test on the groups indicated by the y variable, you could do the following through dplyr:

t.test(dat %>% filter(y=="A") %>% pull(x),
       dat %>% filter(y=="B") %>% pull(x))

## 
## 	Welch Two Sample t-test
## 
## data:  dat %>% filter(y == "A") %>% pull(x) and dat %>% filter(y == "B") %>% pull(x)
## t = -0.52826, df = 14.151, p-value = 0.6055
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -1.3785623  0.8332464
## sample estimates:
##   mean of x   mean of y 
## -0.30767009 -0.03501214

12.2 `dplyr`

dplyr is the Swiss army knife of dataframe manipulation. It can be used to take subsets of the rows of a dataframe on the basis of the values of one or more variables (filter function). It can be used to take subsets of the column of a dataframe (select function). It can be used to create new columns that are functions of one or more rows of a dataframe (mutate function). It can be used to create dataframes that summarize variables of another dataframe on the basis of factor groupings (summarize combined with group_by functions). All these operations could be done also without dplyr through base R functions. However, dplyr really shines in making these operations seamless and straightforward, with a concise sintax.

A key element that allows you to seamlessly manipulate dataframes with dplyr with a concise sintax is the pipe operator %>%. This operator comes from the magrittr package that is automaticaly loaded when you lod dplyr. Let’s suppose that we want to take the subset of the iris dataframe consisting of observations for the species setosa, and we’re only interested in the columns for petal length and width. We can do this without using the pipe operator as follows:

iris_set = filter(iris, Species=="setosa")
iris_set = select(iris_set, Petal.Length, Petal.Width)

when used without the pipe operator, the first argument that we pass to the filter and select functions is the dataframe on which they need to operate. With the pipe we don’t need to pass this argument to the functions, we simply “pipe” the dataframe through as follows:

iris_set = iris %>% filter(Species=="setosa") %>% select(Petal.Length, Petal.Width)

this way we’ve “chained” two operations and accomplised our aim with a single, less verbose, line of code! You can think of the %>% operator as taking the output of the function on its left and passing it forward to the function on its right for further processing.

12.2.1 `group_by` and `summarize`

The group_by function generates a “grouped” tibble:

grIris = iris %>% group_by(Species);
str(grIris)

## tibble [150 × 5] (S3: grouped_df/tbl_df/tbl/data.frame)
##  $ Sepal.Length: num [1:150] 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
##  $ Sepal.Width : num [1:150] 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
##  $ Petal.Length: num [1:150] 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
##  $ Petal.Width : num [1:150] 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
##  - attr(*, "groups")= tibble [3 × 2] (S3: tbl_df/tbl/data.frame)
##   ..$ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 2 3
##   ..$ .rows  : list<int> [1:3] 
##   .. ..$ : int [1:50] 1 2 3 4 5 6 7 8 9 10 ...
##   .. ..$ : int [1:50] 51 52 53 54 55 56 57 58 59 60 ...
##   .. ..$ : int [1:50] 101 102 103 104 105 106 107 108 109 110 ...
##   .. ..@ ptype: int(0) 
##   ..- attr(*, ".drop")= logi TRUE

this is useful because subsequent functions in the pipeline operate on the groups defined with group_by. For example, the following lines will compute the mean petal length for each species:

iris %>% group_by(Species) %>% summarize(meanPetLen=mean(Petal.Length))

## # A tibble: 3 x 2
##   Species    meanPetLen
##   <fct>           <dbl>
## 1 setosa           1.46
## 2 versicolor       4.26
## 3 virginica        5.55

note that we can group by more than one variable, and we can compute more than one statistics in the summarize call, as shown in the following example which uses the mpg dataset provided by ggplot2:

library(ggplot2)
mpg_grpd = mpg %>% group_by(manufacturer, trans) %>% summarize(meanHWY=mean(hwy),
                                                               sdHWY=sd(hwy),
                                                               meanCTY=mean(cty),
                                                               sdCTY=sd(cty))
head(mpg_grpd)

## # A tibble: 6 x 6
## # Groups:   manufacturer [2]
##   manufacturer trans      meanHWY sdHWY meanCTY sdCTY
##   <chr>        <chr>        <dbl> <dbl>   <dbl> <dbl>
## 1 audi         auto(av)      28.5  2.12    19.5  2.12
## 2 audi         auto(l5)      25.8  1.92    16    1.22
## 3 audi         auto(s6)      25    1.63    17.2  1.26
## 4 audi         manual(m5)    26.5  1.73    18.5  1.73
## 5 audi         manual(m6)    28    3       18.3  2.89
## 6 chevrolet    auto(l4)      20.6  5.43    14.7  3.36

12.2.2 Getting counts of cases

y = rnorm(100, mean=100, sd=20)
fct = rep(c("A", "B", "C", "D"), each=25)
dat = data.frame(fct=fct, y=y)
dat %>% group_by(fct) %>% filter(y>100) %>% summarize(n())

## # A tibble: 4 x 2
##   fct   `n()`
##   <chr> <int>
## 1 A        13
## 2 B        16
## 3 C         8
## 4 D        15

## shorthand version
dat %>% filter(y>100) %>% count(fct)

##   fct  n
## 1   A 13
## 2   B 16
## 3   C  8
## 4   D 15

## alternative version
dat %>% group_by(fct) %>% filter(y>100) %>% tally()

## # A tibble: 4 x 2
##   fct       n
##   <chr> <int>
## 1 A        13
## 2 B        16
## 3 C         8
## 4 D        15

12.3 Tests statistics with `dplyr` and `broom`

The broom package converts the output of some R models to tibbles. As we will see below, used in conjunction with dplyr this provides a very efficient way of fitting models or performing statistical tests on grouped data. Let’s first see an example of what broom does. We’ll fit a simple linear regression model using the iris dataset. We’ll first fit the model on the data of the setosa species only:

data(iris)
fit_single = lm(Petal.Length~Sepal.Length, data=iris %>% filter(Species=="setosa"))

if we run str(fit_single) we can see that the output of lm is a list. We can get a nice printout of the results with summary(fit_single), but while easy to read, such output is again stored in a list (you can check with str(summary(fit_single))) which is not easy to store or process further (e.g. combining the output with that of other model fits and storing in a CSV file). broom aims to solve this issue. The tidy function turns the coefficients and test statistics for each term of the model into a tibble:

library(broom)
fit_single_tidy = tidy(fit_single)

the glance function turns parameters and statistics global to the model (as opposed to being specific to a given term) into a tibble:

fit_single_glance = glance(fit_single)

finally the augment function computes statistics such as the fitted values and residuals that can be added back to the input dataframe, thus augmenting it.

iris_aug = iris %>% group_by(Species) %>% summarize(lmfit=augment(lm(Petal.Length~Sepal.Length)))

Combined with dplyr the broom function makes fitting statistical models on grouped data efficient. Below we’ll use again the iris dataset, but we’ll use the whole dataset, fitting a separate model for each iris species in one go:

fit_frame_tidy = iris %>% group_by(Species) %>% summarize(lmfit=tidy(lm(Petal.Length~Sepal.Length)))
fit_frame_glance = iris %>% group_by(Species) %>% summarize(lmfit=glance(lm(Petal.Length~Sepal.Length)))

13 Probability distributions

13.1 The Bernoulli distribution

A random variable $X$ that takes a value of 0 or 1 depending on the result of an experiment that can have only two possible outcomes, follows a Bernoulli distribution. If the probability of one outcome is $p$, the probability of the other outcome will be $p-1$: \[ P(X=1) = p\] \[ P(X=0) = p-1\] The expected value of a Bernoulli random variable is $p$: \[ E[X]= 1\cdot p + 0\cdot p = p\] the variance of a Bernoulli random variable is given by: \[ Var(X) = E[X^2] - E[X]^2 = 1^2\cdot p + 0^2\cdot p - p^2 \] \[Var(X) = p-p^2 = p\cdot(1-p)\]

Figure 13.1 shows the probability mass function of a Bernoulli random variable with $p=0.7$.

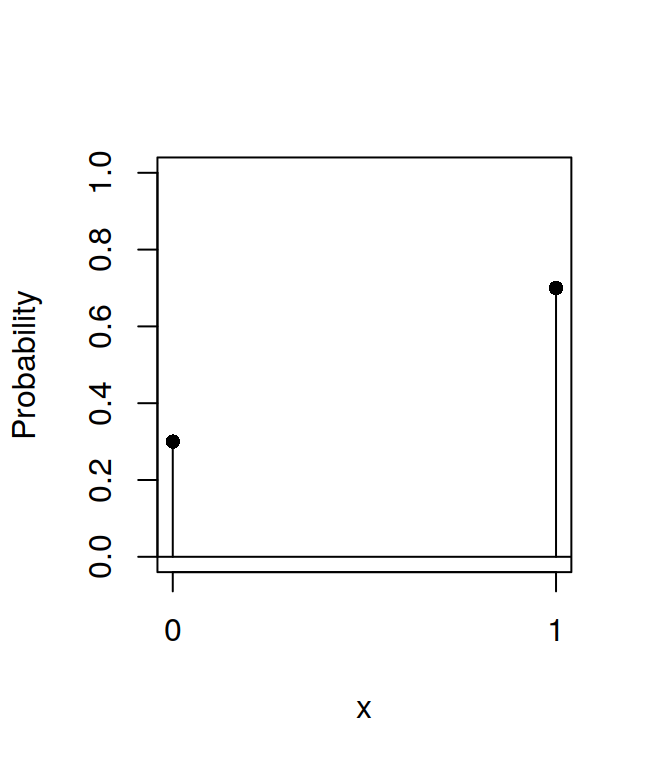
Figure 13.1: Probability mass function for a Bernoulli random variable.

As far as I know, there are no special functions in R for computations related to the Bernoulli distribution (mass function, distribution, and quantile function). However, since the Bernoulli distribution is a special case of the binomial distribution, with the parameter $n$ equal to 1, the R functions for the binomial distribution can be used for the Bernoulli distribution as well. Most of the calculations involved are quite simple anyway. The probability mass function can be calculated as follows:

dbinom(x=0, size=1, prob=0.7)

## [1] 0.3

dbinom(x=1, size=1, prob=0.7)

## [1] 0.7

note that the parameter $n$ of the binomial distribution in R functions is passed through the size argument.

The cumulative distribution function can be computed as follows:

pbinom(q=0, size=1, prob=0.7)

## [1] 0.3

pbinom(q=1, size=1, prob=0.7)

## [1] 1

The quantile function can be computed as follows:

qbinom(p=0.3, size=1, prob=0.7)

## [1] 0

qbinom(p=1, size=1, prob=0.7)

## [1] 1

Finally, one can generate a random sample from a Bernoulli distribution as follows:

rbinom(n=10, size=1, prob=0.7)

##  [1] 0 1 1 1 1 1 0 1 0 1

13.2 The binomial distribution

The binomial distribution with parameters $n$ and $p$ represents the number of “successes” in a sequence of $n$ independent Bernoulli trials, each with a $p$ probability of success. The probability mass function is given by Eq. (13.1): \[\begin{equation} P(X=k) = \dbinom{n}{k} p^k (1-p)^{n-k} \tag{13.1} \end{equation}\] where $k$ is the number of successes. Figure 13.2 shows the probability mass function for a binomial random variable with $n=10$, and $p=0.7$.

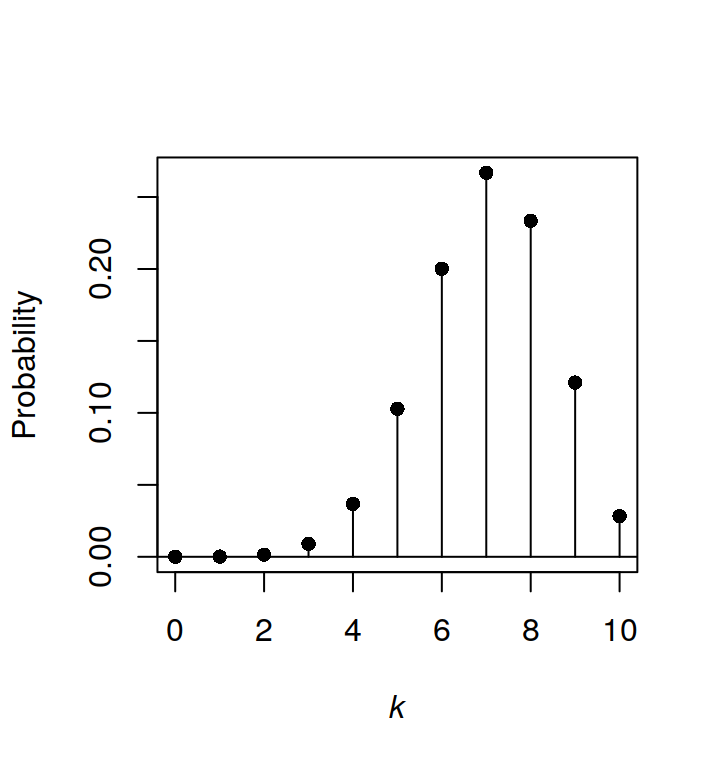
Probability mass function for a binomial random variable with $n=10$ and $p=0.7$. The plot shows the probability of obtaining exactly $k$ successes out of $n$ trials.

Figure 13.2: Probability mass function for a binomial random variable with $n=10$ and $p=0.7$. The plot shows the probability of obtaining exactly $k$ successes out of $n$ trials.

In R the probability mass function can be computed via the dbinom function. For example, the probability of obtaining exactly 7 success out of 10 trials with $p$ for each trial = 0.7 is:

dbinom(x=7, size=10, prob=0.7)

## [1] 0.2668279

The binomial cumulative distribution function represents the probability of obtaining $\leq k$ successes in $n$ trials in which the probability of success for a single trial is $p$. In R it can be computed with the pbinom function. For example, the probability of obtaining $\leq 7$ success in 10 trials, with $p=0.7$ is:

pbinom(q=7, size=10, p=0.7)

## [1] 0.6172172

The quantile function can be computed with the qbinom function:

qbinom(p=pbinom(q=7, size=10, prob=0.7), size=10, prob=0.7)

## [1] 7

Random binomial samples can be obtained with the rbinom function:

rbinom(n=5, size=10, prob=0.7)

## [1] 8 9 7 8 8

note that n here represents the number of samples to draw, while size refers to the number of Bernoulli trials of the binomial distribution.

13.3 The normal distribution

The desnity function for the normal distribution in R is given by dnorm. For example the density function for a value of 0.5 for a normal distribution with a mean of zero and a standard deviation of one can be computed with:

dnorm(x=0.5, mean=0, sd=1)

## [1] 0.3520653

The code below plots a standard normal distribution between -3 and 3 using the dnorm function, and shades its right $0.05\%$ tail. The resulting plot is shown in Figure 13.3.

curve(dnorm(x, 0, 1), from=-3, to=3, ylab="Density.")
coord = seq(from=0+qnorm(.95)*1, to=3, length=30)
dcoord = dnorm(coord, 0, 1)
polygon(x=c(0+qnorm(.95)*1, coord, 3),
        y=c(0, dcoord, 0), col = "skyblue")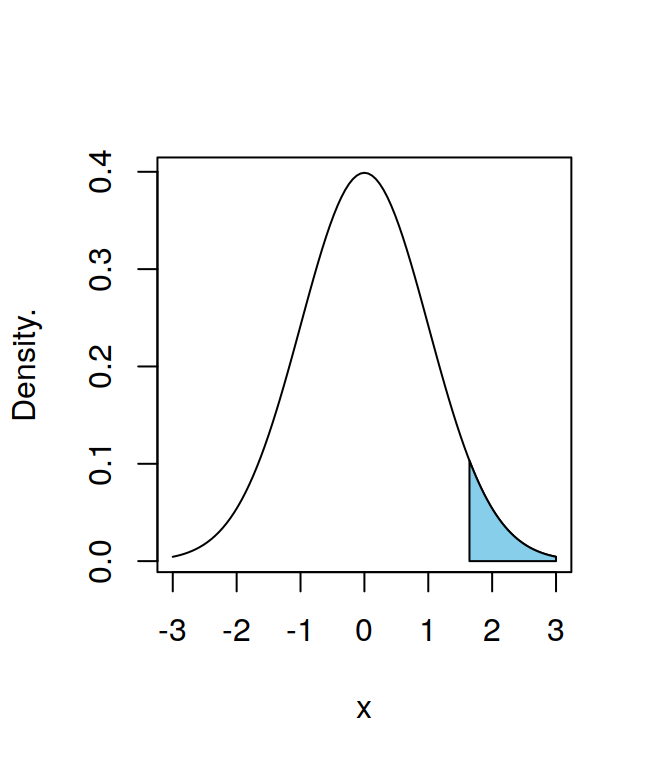

Figure 13.3: The standard normal distribution

The cumulative normal distribution function in R is given by pnorm. For example pnorm can be used to find the probability value associated with a given $z$ point of the standard normal distribution:

pnorm(1.96, mean=0, sd=1)

## [1] 0.9750021

will give the value of the area under the standard normal distribution curve from $-\infty$ to $1.96$.

The quantal function of the normal distribution in R is given by qnorm. For a standard normal distribution, qnorm gives the z point associated with a given probability area under the curve. For example:

qnorm(0.975, mean=0, sd=1)

## [1] 1.959964

13.3.1 Using the normal distribution to run a z-test

We can use the pnorm function to test hypotheses with a z-test. Suppose we have a sample of 40 computer science students with a mean short term memory span of $7.4$ digits (that is, they can repeat in sequence, about $7$ digits you read them, without making a mistake), and standard deviation of $2.3$. The mean for the general population is $6.5$ digits, and the variance in the population is unknown. We’re interested in seeing if the memory span for computer science students is higher than that of the general population. We’ll run a z-test as \[z=\frac{\overline x - \mu_{\overline x} }{\frac{s}{\sqrt{n-1}}}\] where $\overline x$ is the mean short term memory span for our sample, and $s$ is its standard deviation. The z value for our sample is:

z = (7.4-6.5)/(2.3/sqrt(40-1))
z

## [1] 2.443695

we then get the area under the curve from $-\infty$ to our z-value, which gives us the probability of a score lower than $7.4$:

pnorm(z)

## [1] 0.9927311

To get the p-value we subtract that probability value from $1$, this would give us the probability of getting a score equal to or higher than $7.4$ for a one-tailed test. Because we want a two-tailed test instead, we multiply that value by two, to get the p-value.

1-pnorm(z) #this would do for a one tailed test

## [1] 0.007268858

(1-pnorm(z))*2 #p-value for two-tailed test

## [1] 0.01453772

The qnorm command on the other hand, can be used to set confidence limits on the mean, for the example above we would use the following formula: \[CI= \overline x \pm z_{\alpha/2} \frac{s}{\sqrt{n-1}}\] to set a $95\%$ confidence interval on the mean short term memory span for the computer science students:

alpha = 0.05
s = (2.3/sqrt(40-1))
zp = (1-alpha/2)
ciup = 7.4 + zp*s
cilow = 7.4 - zp*s
cat("The 95% CI is: \n", cilow, "<", "mu", "<", ciup, "\n")

## The 95% CI is: 
##  7.040913 < mu < 7.759087

The following code summarizes the situation graphically, as shown in Figure 13.4.

s = (2.3/sqrt(40-1))
up = seq(from = 6.5+qnorm(.975)*s, to = 9.5, length = 30)
low = seq(from =3.5 , to =6.5-qnorm(.975)*s , length = 30)
dup = dnorm(up, 6.5, s)
dlow = dnorm(low, 6.5, s)
curve(dnorm(x, 6.5, s), from= 4.5, to= 8.5, ylab="Density")
polygon(x = c( 6.5+qnorm(.975)*s, up, 9.5),
        y = c(0, dup, 0), col = "orange")
polygon(x = c(3.5,low, 6.5-qnorm(.975)*s),
        y = c(0, dlow, 0), col = "orange")
text(x=c(7.38,5.62), y=c(0.02,0.02), expression(alpha/2))
text(x=c(6.5), y=c(0.3), expression(1-alpha))
lines(x=c(7.8, 7.4), y=c(0.28,0))
text(x=c(7.4), y=c(-0.025), expression(7.4))
text(x=c(7.8), y=c(0.32), "comp. science \ngroup score")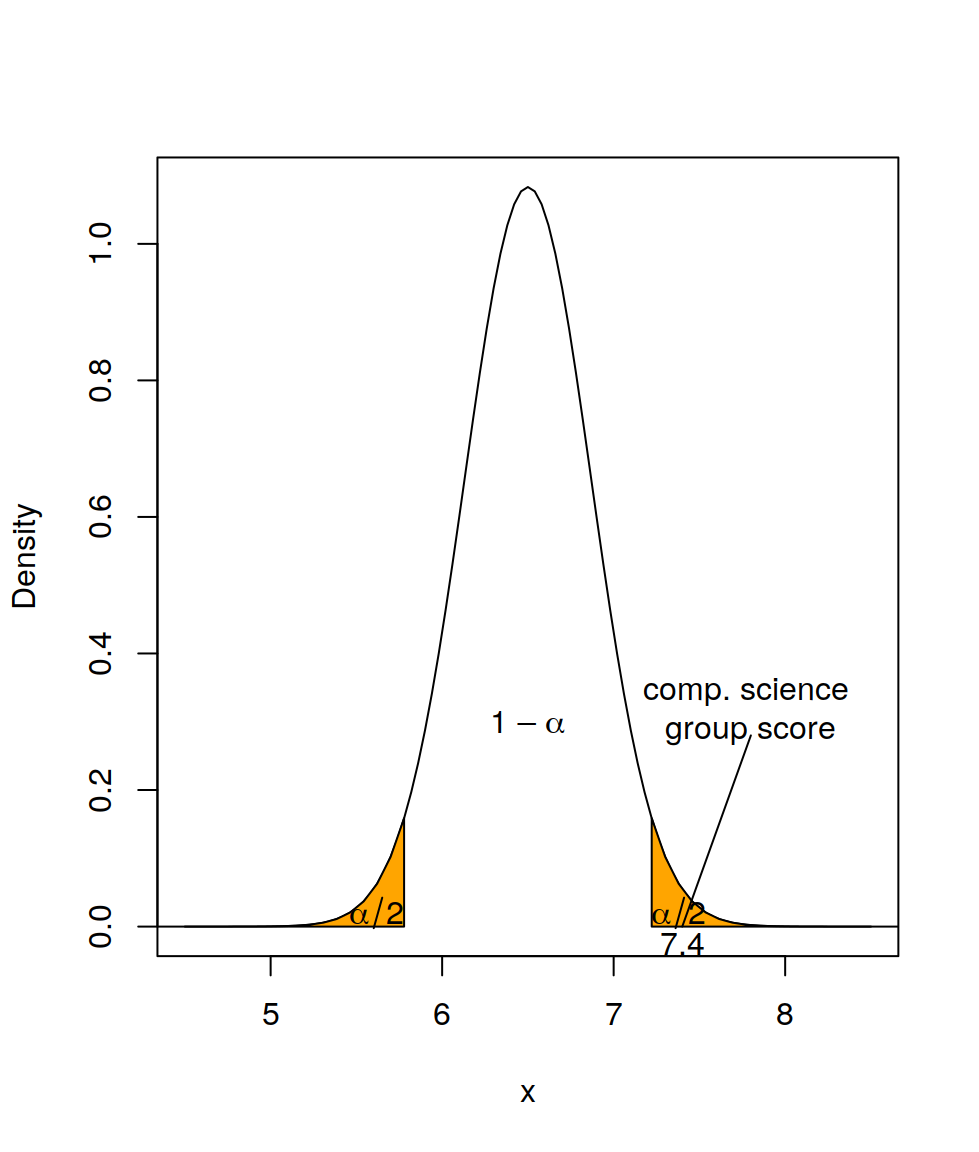

Figure 13.4: Illustration of the z-test for the short term memory span experiment.

13.4 Further resources

13.4.1 Related packages

The distributions3 package provides an alternative interface to computations of functions related to probability distributions.

14 Frequentist hypothesis tests

This is not a statistics textbook. The examples are simply meant to show the syntax to perform certain tests in R, the correct execution of tests and the interpretation of their results depend on good theoretical knowledge of the statistical tests and their assumptions.

14.1 $\chi^2$ test

14.1.1 Testing hypotheses about the distribution of a categorical variable

The $\chi^2$ test can be used to verify hypotheses about the distribution of a categorical variable. For example we might test whether a given population of participants, say guitar players, follows the pattern of handedness found in the general population, known to have a distribution of $80\%$ right-handed, $15\%$ left-handed, and $5\%$ ambidextrous individuals (all the data in this example are made up). The handedness frequencies for a hypothetical sample of guitar players are given in Table 14.1

Table 14.1: Table of handedness frequencies for a sample of guitar players.
Right	Left	Both	Total
93	18	2	113

we can run the test with the following command:

chisq.test(x=c(93,18,2), p=c(0.8,0.15,0.05))

## 
## 	Chi-squared test for given probabilities
## 
## data:  c(93, 18, 2)
## X-squared = 2.4978, df = 2, p-value = 0.2868

we give the function a vector x with the handedness counts for each category in our sample of guitar players, and a vector p of the expected frequencies for each category in the general population. R returns the value of the $\chi^2$ statistics and its associated p-value. In our case, assuming $\alpha=0.05$, the p-value indicates that the $\chi^2$ statistics is not significant, , therefore we do not reject the null hypothesis that the distribution of handedness in the population of guitar players differs from that of the general population.

14.1.2 Testing hypotheses about the association between two categorical variables

The $\chi^2$ test can also be used to verify a possible association between two categorical variables, for example sex and cosmetic products usage (classified as “high”, “medium” or “low”). A contingency table showing hypothetical data on cosmetic usage for a sample of $44$ males and $67$ females is shown in Table 14.2.

Table 14.2: Cosmetic usage by sex.
	High	Medium	Low	Total
Males	$6$	$11$	$27$	$44$
Females	$25$	$30$	$12$	$67$
Total	$31$	$41$	$39$	$111$

The formula for the $\chi^2$ statistics is \[\begin{equation} \chi^2=\sum\frac{(f_e - f_o)^2}{f_e} \tag{14.1} \end{equation}\]

where $f_e$ are the expected frequencies and $f_o$ are the observed frequencies. In order to get the statistics and perform a test of significance on it with R we can first arrange the data in a matrix:

cosm = c(6, 11, 27, 25, 30, 12)
cosm = matrix(cosm, nrow=2, byrow=TRUE)

then we can pass the matrix to the chisq.test() function to test the null hypothesis that there is no association between sex and cosmetic usage:

chisq.test(cosm)

## 
## 	Pearson's Chi-squared test
## 
## data:  cosm
## X-squared = 22.416, df = 2, p-value = 1.357e-05

the p-value tells us that the null hypothesis does not hold, there is indeed an association between sex and degree of cosmetic usage. If we store the results of the test in a variable, we’ll be able to get the matrices of the expected frequencies and residuals:

cosmtest = chisq.test(cosm)
cosmtest$expect ## expected frequencies under a true null hypothesis

##          [,1]     [,2]     [,3]
## [1,] 12.28829 16.25225 15.45946
## [2,] 18.71171 24.74775 23.54054

If we have only a few observations and want to use the Yate’s correction for continuity we have to set the optional argument correct to TRUE:

chisq.test(x=mydata, correct=TRUE)

Often we might not have the data already tabulated in a contingency table, however if we have a series of observations classified according to two categorical variables we can easily get a contingency table with the table() function. The next example uses the data in the file hair_eyes.txt, that lists the hair and eyes colors for 260 females. We will first build our contingency table from that:

dat = read.table("datasets/hair_eyes.txt", header=TRUE)
tabdat = table(dat$hair, dat$eyes)

now we can perform the $\chi^2$ test directly on the table to test for an association between hair and eyes color:

chisq.test(tabdat)

## Warning in chisq.test(tabdat): Chi-squared approximation may be incorrect

## 
## 	Pearson's Chi-squared test
## 
## data:  tabdat
## X-squared = 142.9, df = 9, p-value < 2.2e-16

the $\chi^2$ statistics is significant, suggesting an association between hair and eyes color.

14.2 Student’s t-test

14.2.1 One sample t-test

A one-sample t-test can be used to test if a group mean is significantly different from a given, known, population mean ($\mu$). The following example simulates some data and runs a one-sample t-test of the hypothesis that the group mean is equal to a known population mean of 18:

set.seed(938) #set random seed
gr1 = rnorm(20, mean=20, sd=4) #simulate data
t.test(gr1, mu = 18)

## 
## 	One Sample t-test
## 
## data:  gr1
## t = 3.0375, df = 19, p-value = 0.006774
## alternative hypothesis: true mean is not equal to 18
## 95 percent confidence interval:
##  18.65846 21.57681
## sample estimates:
## mean of x 
##  20.11763

For the example we simulated data from a normal distribution with a mean of 20, so unsurprisingly the null hypothesis that the group mean is equal to 18 is rejected at the 0.05 alpha level. By default the test is run as a two-sided test, but this can be changed by passing the alternative argument (valid options for this argument are: two-sided, less, greater). For example, to test the hypothesis that the group mean is > 18 we would call the function as follows:

t.test(gr1, mu=18, alternative="greater")

## 
## 	One Sample t-test
## 
## data:  gr1
## t = 3.0375, df = 19, p-value = 0.003387
## alternative hypothesis: true mean is greater than 18
## 95 percent confidence interval:
##  18.91215      Inf
## sample estimates:
## mean of x 
##  20.11763

By default the output reports the bounds of a 95% confidence interval on the group mean. The confidence level of this interval can be changed via the conf.level argument. For example, to print out a 99% confidence interval:

t.test(gr1, mu = 18, conf.level=0.99)

## 
## 	One Sample t-test
## 
## data:  gr1
## t = 3.0375, df = 19, p-value = 0.006774
## alternative hypothesis: true mean is not equal to 18
## 99 percent confidence interval:
##  18.12310 22.11216
## sample estimates:
## mean of x 
##  20.11763

14.2.2 Two-sample t-test

A two-sample t-test can be used to test whether there is a significant difference between the means of two groups. In the following example we’ll simulate data for the two groups and run the test:

gr1 = rnorm(25, mean=10, sd=2)
gr2 = rnorm(25, mean=8, sd=2)
t.test(gr1, gr2)

## 
## 	Welch Two Sample t-test
## 
## data:  gr1 and gr2
## t = 3.3003, df = 46.562, p-value = 0.001858
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  0.7978221 3.2906509
## sample estimates:
## mean of x mean of y 
##  9.821537  7.777301

as for the one-sample t test described in the previous section it is possible to run either a two-sided (the default) or a directional one-sided test via the alternative argument, and it is also possible to set the confidence level for the confidence interval reported via the conf.level argument. An additional argument that can be passed for a two-sample t-test is var.equal, if this is set to TRUE, then the variances of the two groups are treated as being equal, and the pooled variance is used to estimate the variance otherwise the Welch (or Satterthwaite) approximation to the degrees of freedom is used (Derrick, Toher, and White 2016). One way to decide whether to treat the variances of the two groups as equal is by running the Levene test for homogeneity of variances which is described in Section 14.3.

14.2.3 Paired t-test

A paired sample t-test can be used to test whether the means of the same group of participants differ between two conditions. We’ll simulate again some data and run the test:

base = rnorm(30, mean=0, sd=5)
cnd1 = base + rnorm(30, mean=-2, sd=2.5)
cnd2 = cnd1 + rnorm(30, mean=2, sd=2.5)
t.test(cnd1, cnd2, paired=TRUE)

## 
## 	Paired t-test
## 
## data:  cnd1 and cnd2
## t = -4.4552, df = 29, p-value = 0.0001149
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -2.995939 -1.110716
## sample estimates:
## mean of the differences 
##               -2.053328

as for the one-sample t test described previously it is possible to run either a two-sided (the default) or a directional one-sided test via the alternative argument, and it is also possible to set the confidence level for the confidence interval reported via the conf.level argument.

A paired t-test could also be calculated as a one-sample t-test on the difference between the scores in the two conditions:

t.test(cnd1-cnd2, mu=0)

## 
## 	One Sample t-test
## 
## data:  cnd1 - cnd2
## t = -4.4552, df = 29, p-value = 0.0001149
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  -2.995939 -1.110716
## sample estimates:
## mean of x 
## -2.053328

14.3 The Levene test for homogeneity of variances

The Levene test can be used to test if the variances of two samples are significantly different from each other. This procedure is important because some statistical tests, such as the two independent sample t-test, are based on the assumption that the variances of the samples being tested are equal. In R the function to perform the Levene test is contained in the car package, so in order to call it the package must be installed and the car library has to be loaded with the command:

library(car)

We’ll first simulate some data:

y1 = rnorm(25, mean=0, sd=1)
y2 = rnorm(25, mean=0, sd=2)
y = c(y1, y2)
grps = factor(rep(c("A", "B"), each=25))

we need a vector (y in our case) with the values of the dependent variable that we are measuring, and another vector (grps in our case) defining the group to which a given observation belongs to. We can then run the test with:

leveneTest(y, grps)

## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value   Pr(>F)   
## group  1   9.787 0.002986 **
##       48                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We’ll present another example with three groups. Let’s imagine that in a verbal memory task we have the measures (number of words recalled) of three groups that have been given three different treatments (e.g. three different rehearsal procedures). We want to see if there are significant differences in the variance between the groups. The data are stored in a text file verbal.txt, as in Table 14.3, but with no header indicating the column names.

Table 14.3: Data for the Levene test example.
Procedure 1	Procedure 2	Procedure 3
12	13	15
9	12	17
9	11	15
8	7	13
7	14	16
12	10	17
8	10	12
7	10	16
10	12	14
7	9	15

First we will create the vector with the values of the dependent variables, by reading in the file with the scan function:

values = scan("datasets/verbal.txt")

Now we need to create a second vector defining the group to which a given observation on the data vector belongs to. We will use the rep function to do this, and for convenience we’ll give the labels 1, 2 and 3 to the three groups:

groups = factor(rep(1:3, 10))

Now the data are in a proper format for using the leveneTest function. This format can be called the “one row per observation” format. You can find more info on this format in Section 3.8.1. To perform the test we can use the following commands:

leveneTest(values, groups)

## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  2  0.3391 0.7154
##       27

As you can see we have an F value with its associated p value, if the p value is significant, then we reject the null hypothesis of equal variances between the groups. In our case below the p value is greater than 0.05 so we cannot reject the null hypothesis that the variances in the three groups are equal.

14.4 Analysis of variance

We’ll start with an example showing how we can perform a one-way between-subjects analysis of variance (ANOVA) in R. The example uses a dataset from a fictitious experiment on the effect of three types of memory-boosting drugs. Thirty participants were randomly assigned to one of three groups, each given a different memory-boosting drug (drug “A”, “B”, or “C”), and afterwards their memory was assessed by counting the number of words they could recall from a list. The data is shown in Table 14.4.

Table 14.4: Number of words recalled from a list for participants treated with drug A, B, or C.
Drug A	Drug B	Drug C
12	13	15
9	12	17
9	11	15
8	7	13
7	14	16
12	10	17
8	10	12
7	10	16
10	12	14
7	9	15

We read in the dataset:

drug_mem = read.table("datasets/drug_memory.csv", header=T, sep=",")
head(drug_mem)

##   n_words drug
## 1      12    A
## 2      13    B
## 3      15    C
## 4       9    A
## 5      12    B
## 6      17    C

the dependent variable is the number of words correctly recalled from the list (n_words), while the other column (drug) denotes the experimental group. We can have a look at the data through a dotplot:

library(ggplot2)
p = ggplot(drug_mem, aes(drug, n_words)) + geom_point()
p = p + xlab("Drug") + ylab("# words recalled")
p = p + theme_bw()
print(p)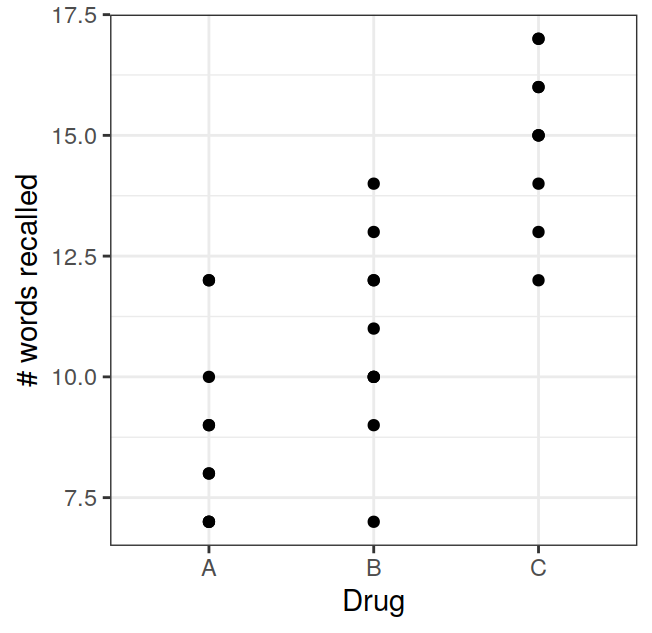

Figure 14.1: Number of words recalled for participants administered different types of memory-boosting drugs.

the dotplot, shown in Figure 14.1, suggests that the drugs have different effects on the number of recalled words. We can run the ANOVA with the aov function:

drug_mem_aov = aov(n_words ~ drug, data=drug_mem)

the first argument passed to the function is the model formula, which you can read as “explain n_words as a function of drug”; the other argument, data, is the dataframe containing the data. Calling summary on the aov output gives a pretty printout with various info we need to report the results (degrees of freedom, F value, p-value, etc…)

summary(drug_mem_aov)

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## drug         2  194.9   97.43   27.84 2.75e-07 ***
## Residuals   27   94.5    3.50                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

assuming a significance level of 0.05 the results of the test reject the null hypothesis that the three drugs have the same effectiveness on the number of recalled words from a list.

Another function that can run a one-way ANOVA in R is oneway.test. Its syntax is very similar to that of aov, but it has an additional argument, var.equal, to indicate whether homogeneity of variance should be assumed or not. If not, a Welch-type test is run (see ?oneway.test). For example, if we had reason to suspect non-homogeneous variances across the groups we could have run the test with:

oneway.test(n_words ~ drug, data=drug_mem, var.equal=F)

## 
## 	One-way analysis of means (not assuming equal variances)
## 
## data:  n_words and drug
## F = 30.598, num df = 2.000, denom df = 17.831, p-value = 1.719e-06

The aov function is quite flexible, and can handle multiple factors. For example, the syntax to run an ANOVA on a dependent variable y with two factors fct1 and fct2 stored in a dataframe called dat would be:

aov(y ~ fct1*fct2, data=dat)

the above would estimate the effects of fct1, fct2, and their interaction. It would also be possible to estimate only the main effects, without the interaction term, if desired, with the following syntax:

aov(y ~ fct1+fct2, data=dat)

The syntax for performing repeated measures ANOVA with aov becomes relatively complex because it is necessary to specify appropriate error strata. This is explained in detail in Baron and Li (2003), and Li and Baron (2012). The ez package provides an easier interface for running ANOVAs, and for this reason we’ll focus on it.

The function to run ANOVAs through the ez package is called ezANOVA and we’ll first show how to use it by running the one-way between-subjects ANOVA that we ran earlier with aov. The ezANOVA function requires a subject identifier even for between-subjects designs, so we’ll add one to the drug_mem data. Each observation came from a different participant, so we’ll simply label the participants as P1, P2, P3, etc…:

drug_mem$id = factor(paste0("P", 1:dim(drug_mem)[1]))

next we load the ez package and run the ANOVA:

library(ez)
ezANOVA(drug_mem, dv=n_words, between=drug, wid=id)

## Warning: Converting "drug" to factor for ANOVA.

## $ANOVA
##   Effect DFn DFd       F            p p<.05       ges
## 1   drug   2  27 27.8381 2.746469e-07     * 0.6734247
## 
## $`Levene's Test for Homogeneity of Variance`
##   DFn DFd       SSn  SSd         F         p p<.05
## 1   2  27 0.8666667 34.5 0.3391304 0.7153804

the first argument passed to the ezANOVA function is the dataframe holding the data, the second argument dv, is the name of the dependent variable, the between argument is used to pass the names of the between-subject factor(s), and the wid argument is used to pass the name of the variable holding the subject identifiers. The syntax for specifying multiple factors is a bit unusual (but not difficult). For example, if in the above example we had a second between-subject factor called dose, to use both factors in the analysis we would have written between=.(drug, dose). We’ll see a concrete example with the ToothGrowth dataset. In the dataset dose is a numeric variable; for this example we’ll treat it as a factor, and therefore, after loading the dataset, the code below converts it to a factor:

data(ToothGrowth)
ToothGrowth$dose = factor(ToothGrowth$dose)
ToothGrowth$id = factor(paste0("P", 1:dim(ToothGrowth)[1]))

again, we added a subject identifier to the dataset, and we’re now ready to run the analysis with the code below:

ezANOVA(ToothGrowth, dv=len, between=.(supp, dose), wid=id)

## Coefficient covariances computed by hccm()

## $ANOVA
##      Effect DFn DFd         F            p p<.05       ges
## 1      supp   1  54 15.571979 2.311828e-04     * 0.2238254
## 2      dose   2  54 91.999965 4.046291e-18     * 0.7731092
## 3 supp:dose   2  54  4.106991 2.186027e-02     * 0.1320279
## 
## $`Levene's Test for Homogeneity of Variance`
##   DFn DFd    SSn     SSd        F         p p<.05
## 1   5  54 38.926 246.053 1.708578 0.1483606

In order to run repeated measures ANOVAs, in which there are one or more within-subject factors we need to list these factors in the within argument. For example, the following dataset contains data from a fictitious experiment on the effects of a drug and of alcohol on social interaction in rats. Two species of rats were tested (the between-subject factor group). Each rat was tested with or without the drug, and with or without alcohol. The dependent measure was the number of social interactions recorded by the experimenter. The fictitious data are in the socialint_drug_alcohol_species.csv dataset:

dat = read.table("datasets/socialint_drug_alcohol_species.csv",
                 header=T, sep=",", stringsAsFactor=T)

next we run the ANOVA with the code below:

ezANOVA(dat, dv=socialint,
        between=.(group),
        within=.(drug, alcohol),
        wid=id,
        type="3")

## Warning: Converting "id" to factor for ANOVA.

## $ANOVA
##               Effect DFn DFd            F            p p<.05          ges
## 2              group   1  14 4.615385e-01 5.079831e-01       2.290076e-02
## 3               drug   1  14 8.104819e+01 3.376241e-07     * 3.848618e-01
## 5            alcohol   1  14 2.276577e+01 2.982114e-04     * 1.903005e-01
## 4         group:drug   1  14 6.831325e+00 2.042593e-02     * 5.009276e-02
## 6      group:alcohol   1  14 6.306306e-02 8.053669e-01       6.506181e-04
## 7       drug:alcohol   1  14 1.600000e+01 1.316049e-03     * 4.000000e-02
## 8 group:drug:alcohol   1  14 4.437343e-31 1.000000e+00       1.155558e-33

note that we added a type argument, this specifies the sum of squares type to be used for the analysis. In balanced designs, in which you have equal numbers of observations per cell this won’t make a difference, but for unbalanced designs it does. There is some controversy over the most appropriate sum of squares type to use, and the most appropriate choice may depend on the goals and the context of the sudy/analysis. You can read more about the different sum of square types here.

15 Correlation and regression

The function cor can be used to compute Pearson’s $r$ correlation coefficient. For example, using the iris dataset we can compute the correlation between petal length and petal width for the setosa iris species as follows:

data(iris)
iris_setosa = iris[iris$Species == "setosa",]
cor(iris_setosa$Petal.Length, iris_setosa$Petal.Width)

## [1] 0.33163

Kendall’s $\tau$, or Spearman’s $\rho$ rank correlation coefficients can be obtained with the same function by changing the method argument from its default value (pearson) to kendall, or spearman, e.g.:

cor(iris_setosa$Petal.Length, iris_setosa$Petal.Width, method="kendall")

## [1] 0.2217029

A significance test on the correlation coefficient can be obtain with the cor.test function:

cor.test(iris_setosa$Petal.Length, iris_setosa$Petal.Width)

## 
## 	Pearson's product-moment correlation
## 
## data:  iris_setosa$Petal.Length and iris_setosa$Petal.Width
## t = 2.4354, df = 48, p-value = 0.01864
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.05870091 0.55842995
## sample estimates:
##     cor 
## 0.33163

If we pass a matrix or dataframe to the cor function, it will compute the correlations between each pair of columns of the matrix/dataframe:

cor(iris_setosa[, 1:4])

##              Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length    1.0000000   0.7425467    0.2671758   0.2780984
## Sepal.Width     0.7425467   1.0000000    0.1777000   0.2327520
## Petal.Length    0.2671758   0.1777000    1.0000000   0.3316300
## Petal.Width     0.2780984   0.2327520    0.3316300   1.0000000

in the code above we selected columns 1-4 to remove the non-numerical column specifying the iris species. The cor.test function, however, cannot be passed a matrix or dataframe as input. The rcorr function in the Hmisc package can be used to compute correlations and significance tests between all the columns of a matrix:

corr_mat = Hmisc::rcorr(as.matrix(iris_setosa[,1:4]))
corr_mat$r # correlation coefficients

##              Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length    1.0000000   0.7425467    0.2671758   0.2780984
## Sepal.Width     0.7425467   1.0000000    0.1777000   0.2327520
## Petal.Length    0.2671758   0.1777000    1.0000000   0.3316300
## Petal.Width     0.2780984   0.2327520    0.3316300   1.0000000

corr_mat$P # corresponding p-values

##              Sepal.Length  Sepal.Width Petal.Length Petal.Width
## Sepal.Length           NA 6.709842e-10   0.06069778  0.05052644
## Sepal.Width  6.709842e-10           NA   0.21697892  0.10382114
## Petal.Length 6.069778e-02 2.169789e-01           NA  0.01863892
## Petal.Width  5.052644e-02 1.038211e-01   0.01863892          NA

note that rcorr can compute only Pearson’s $r$ or Spearman’s $\rho$ correlation coefficients, by passing an argument named type (rather than method, as for the cor function).

Functions to compute partial, and semi-partial correlations are available in the ppcor package.

15.1 Linear regression

Regression models are expressed in R with a symbolic syntax that is clean and convenient. If you have a dependent variable rts and you want to check the influence of an independent variable age on it, this would be expressed as:

rtfit = lm(rts ~ age)
plot(rts ~ age)
abline(rtfit)

if you want to add another predictor score

rtfit2 = lm(rts ~ age + score)

16 Adjusting the p-values for multiple comparisons

The base R program comes with a number of functions to perform multiple comparisons. Not all the possible procedures are available, and some of them might not be applicable to the object resulting from the specific analysis you’re doing. Additional packages might cover your specific needs.

16.0.0.1 The `p.adjust` function

The function p.adjust comes with the base R program, in the package package stats, so you don’t need to install anything else on your machine apart from R to get it. This function takes a vector of p-values as an argument, and returns a vector of adjusted p-values according to one of the following methods:

holm
hochberg
hommel
bonferroni
BH
BY
fdr
none

So, if for example you’ve run 3 t-test after a one-way ANOVA with 3 groups, to compare each mean group’s mean with the others, and you want to correct the resulting p-values with the Bonferroni procedure, you can use p.adjust as follows:

ps = c(0.001, 0.0092, 0.037) #p values from the t-tests
p.adjust(ps, method="bonferroni")

## [1] 0.0030 0.0276 0.1110

the last line of the example gives the p-values corrected for the number of comparisons made (3 in our case), using the Bonferroni method. As you can see from the output, the first 2 values would still be significant after the correction, while the last one would not.

You can use any of the procedures listed above, instead of the Bonferroni procedure, by setting it in the method option. If you don’t set this option at all you get the Holm procedure by default. Look up the Reference Manual for further information on these methods.

The method none returns the p-values without any adjustment.

16.0.0.2 The `mt.rawp2adjp` function

The package multtest contains a function very similar to p.adjust, and offers some other correction methods.

library(multtest)
ps = c(0.001, 0.0092, 0.037) #p values from the t-tests
mt.rawp2adjp(ps, proc="Bonferroni")

## $adjp
##        rawp Bonferroni
## [1,] 0.0010     0.0030
## [2,] 0.0092     0.0276
## [3,] 0.0370     0.1110
## 
## $index
## [1] 1 2 3
## 
## $h0.ABH
## NULL
## 
## $h0.TSBH
## NULL

or, if you want to see the adjusted p-values with more than one method at once:

library(multtest)
ps <- c(0.001, 0.0092, 0.037) #p values from the t-tests
mt.rawp2adjp(ps, proc=c("Bonferroni", "Holm", "Hochberg", "SidakSS"))

## $adjp
##        rawp Bonferroni   Holm Hochberg     SidakSS
## [1,] 0.0010     0.0030 0.0030   0.0030 0.002997001
## [2,] 0.0092     0.0276 0.0184   0.0184 0.027346859
## [3,] 0.0370     0.1110 0.0370   0.0370 0.106943653
## 
## $index
## [1] 1 2 3
## 
## $h0.ABH
## NULL
## 
## $h0.TSBH
## NULL

17 Administration and maintenance

17.1 Environment customisation

Probably the best way to customise your R environment is through the use of a .Rprofile file, that you put in your HOME directory. This is a simple text file that is sourced every time R is started, so you can put in it your own functions, and any operations that you would like R to perform at start-up. Also in this file, you can write two special functions, the .First is executed first at the beginning of a session, and the .Last is executed at the end of a session. The .First function is normally used to initialise the environment setting the desired options. Here’s an example of a .Rprofile file

##This is my .Rprofile in ~/
.First <- function(){
    options(prompt=">>> ", continue="+\t")  ##change the prompt
    options(digits=5, length=999)           ##display max 5 digits
}

setwd("~/rwork")   ##Start R in this directory

for a full listing of the options that can be set see ?options. You can change temporarily the options, only for the running session, directly from R, for example:

options(digits=9)

The .Rprofile file in the user’s HOME is only one of the files that can be used to initialise the environment and set the options. The file that is looked up first by R is the one defined by the R_PROFILE environment variable if this variable is set. To verify the value of this variable you can use

Sys.getenv("R_PROFILE")

## [1] ""

system("echo $R_PROFILE")

if the variable is unset, R looks for a file called Rprofile.site that is in the etc sub-directory of your R installation directory. To find out your R installation directory on a Unix-like system you can use

system("echo $R_HOME")

The Rprofile.site or the file pointed to by the R_PROFILE environment variable can be used for system-wide configuration. Note that if the R_PROFILE environment variable is set the file pointed to by this variable is used, and if this is not Rprofile.site, the latter is ignored.

The .Rprofile file in the user’s HOME can be used for user specific initialisation, and the functions written in this file overwrite, or better “mask” functions with the same name defined in either the file pointed to by the R_PROFILE variable or in Rprofile.site. Moreover a .Rprofile file can be put in any directory, then, if R is started from that directory, this file is sourced, and it masks the definitions given in the user’s HOME .Rprofile file, in this way, it is possible to customise the initialisation for a particular data analysis. Finally, a directory specific initialisation can be given in a .RData file, the definitions given here mask also the definitions given in any .Rprofile files.

17.2 Compiling R on Debian/Ubuntu

get all the dependencies needed:

apt-get build-dep r-base-core

run configure:

./configure --prefix=/path/to/install_loc/ \
--with-cairo --with-jpeglib \
--with-readline --with-tcltk \
--enable-R-profiling --enable-R-shlib \
--enable-memory-profiling \
--with-blas --with-lapack

--prefix can be used to indicate the directory where R will be installed.

make -j8
make install

If you don’t have some development graphics libraries installed in your system R may nonetheless compile fine, but some functionality may be missing. For example you may have issues with missing fonts (a workaround for this issue is to install gsfonts-x11 and restart the X server or the computer, but the fonts you get by compiling R with all the needed development libraries look better).

18 ESS: Using Emacs Speaks Statistics with R

If you have the Emacs Speaks Statistics (ESS) package installed, you can use Emacs for both editing R source files when working in batch mode, and running a R process from within Emacs. ESS provides an extended set of facilities for both these tasks, among these are syntax highlighting, indentation of code and the ability to work with multiple buffers.

To get syntax highlighting, just use the .R extension for naming your file.

To start an R session from within Emacs, press M-x, type R in the minibuffer, and press Enter.

Another way of running an R session from inside Emacs is to run first a shell in Emacs (press M-x and then type shell in the minibuffer), and then calling R from that shell. However, this doesn’t involve ESS, so you won’t have all the features that ESS adds to the Emacs editing facilities.

For sake of clarity, the use of ESS for editing R source files, and for running a R session will be addressed in two separate sections; however, this separation is quite artificial, first because the most proficient use of ESS involves editing an R source file while running an R session, and second because some of the tips given in one section apply also to the usage of ESS illustrated in the other section. Therefore you’re invited to at least skim through both sections, even if you’re interested on one usage of ESS only.

18.1 Using ESS for editing and debugging R source files

If you have a basic knowledge of Emacs you will feel at home with ESS. A good way to use ESS is to split the Emacs window horizontally (C-x 2) and have a R source file in one buffer, and a R process running in the other buffer. You basically write the R code in the first buffer, and then send it to the R process for evaluation in the second buffer. Below are the shortcuts for sending input to the R process:

C-c C-b Evaluate buffer. This means that all the commands present in the source file will be executed
C-c C-j Evaluate only the current line
C-c C-r Evaluate selected region

There is a set of commands that is equivalent to the above, but moves the cursor to the R process window after the evaluation, that is they `Evaluate and go’ (to the other window):

C-c M-b Evaluate buffer and go
C-c M-j Evaluate line and go
C-c M-r Evaluate region and go

To comment/uncomment a region you can use

M-x comment-region Comment region
M-x uncomment-region Uncomment region
M-; Comment/Uncomment region

If you want to switch from a buffer to the other one you can use C-x o. Moreover, when you are in a buffer you can make the other window scroll without moving the cursor with C-M-v.

18.1.0.1 Italian keyboard mapping issues

Italian keyboards (usually) don’t have the braces { } and some other symbols like the tilde ~, however, on Linux systems, if you’ve chosen an Italian keyboard layout they’re mapped somewhere, and you can access them through a combination of keys, likely combinations are:

Shift + AltGr + [   for {
Shift + AltGr + ]   for }
AltGr + ^           for ~

if you still can’t find them, try pressing AltGr with some keys in the upper part of the keyboard, and see if you can spot them.

In Microsoft Windows the braces { } can be accessed as above, while to access the tilde in most applications, including the R console, you have to write the ASCII code 126 with some modifier function key (in my laptop that’s Alt+Fn 126). In Emacs, however, you can’t write the tilde in this way, a solution is to write the character in octal code by typing:

Ctrl-q 176 RETURN

18.2 Using ESS to interact with a R process

To start a R process type M-x R. C-p and C-n, or C-↑ and C-↓ are for scrolling through the command history.

One thing you need to know, is the ESS “smart underscore” behaviour, that is if you press the underscore once, you get the assignment operator <-, if you press the underscore twice you get a literal underscore _. This shortcut for the assignment operator can be very annoying if you use the underscore often in variable names, to turn-off this smart behaviour you need to put the following line somewhere in your .emacs file, but before ESS is loaded:

(ess-toggle-underscore nil)

When you are running R inside Emacs, if the cursor is not positioned at the current command line, and you try to retrieve some command from the command history with C-p or C-↑, Emacs will complain saying that you are “not at command line”. To get at the command line without using the mouse, press M-Shift->.

If you set the cursor at a previous command, and then press `Enter}, that command will be evaluated again.

There is a quick way to source a file, C-c C-l filename will load and source your file.

C-c C-q is another way of quitting R in ESS mode, but I guess C-d is the fastest one.

19 Writing reports with `rmarkdown` or Sweave

19.1 `rmarkdown`

https://bookdown.org/yihui/rmarkdown/

19.2 Using Sweave to write documents with R and LaTeX

19.2.1 What is Sweave?

Sweave provides a way of writing documents or reports that contain both text and R objects, namely figures, syntax and raw or nicely formatted output produced by R. Sweave is also a way to automate the production of documents. Usually when you write a document with some statistical content, you first write the text, and then add the graphics produced by some statistical software or spreadsheet application. Of course this process is time consuming, not to mention the fact that often you have to manually fill in tables with the statistics produced by the application you’re using. Even worse, if you’ve already prepared your report, but then you have to change something in the statistical analyses, for example you have to add or drop a subject, the entire process must be repeated again from scratch. Sweave is aimed at easing this process, it works like this: you write a single source file which contains your text, written with the LaTeX markup language, and embed in it the R syntax needed for producing the figures and tables to appear in your document. You process this file with Sweave through R, and you get a plain LaTeX source file which you can compile with LaTeX to get your nicely formatted output. If your data happen to change for any reasons, you don’t have to start again from scratch, you can just run your old Sweave source file on your new dataset, and everything will be automatically updated.

If you already know how to use LaTeX and R, learning to use Sweave will be easy, the additional syntax required by Sweave to integrate R and LaTeX source code is minimal.

19.2.2 Usage

R come with Sweave already in the base system (in the package utils), so you don’t need to install it separately. Of course you need LaTeX installed to produce the document later, Sweave only outputs a LaTeX source file and all the graphics needed for your document.

You start the Sweave source file as a normal LaTeX document with the usual preamble, if you name the file with the .Rnw extension, Emacs should recognise it and highlight the syntax for you. Then, at the point where you want to embed a chunk of R syntax, you add the following tag:

<<>>=

after you’ve finished with the R syntax chunk, you need to add the following tag to start another piece of text written with LaTeX:

in this way you can alternate chunks of R code with pieces of LaTeX syntax. If you forget to add the @ tag before a piece of LaTeX syntax Sweave will complain and abort the process, if you instead make a mistake with LaTeX syntax, Sweave won’t complain and will normally produce the .tex file, however the compilation with LaTeX won’t work.

There are different options that determine which R objects will appear in the final document. If you want both the R code, and its output to appear in the document, just use the <<>>= empty tag. They will both be inserted in the LaTeX file in a redefined verbatim environment. Setting the option echo=FALSE lines of R code are not included in the document, while with the option results=hide the output of the R code won’t appear in the document. Therefore if you want to run some R code, but neither the code nor its output should appear in the document, use:

<<echo=FALSE, results=hide>>=

Another option will suppress all the output, except the figures:

<<echo=FALSE, fig=TRUE>>=

Sweave will automatically put a \includegraphics{} command for a figure.

Finally, if you want to use some utilities, like xtable, that automatically produce LaTeX objects from R objects, you will want to use the following options to tell Sweave not to put the R output in a verbatim environment:

<<echo=FALSE, results=tex>>=

20 Sound processing

20.1 Libraries for sound analysis and signal processing

20.1.1 `seewave`

The package seewave provides functions for analysing, manipulating, displaying, editing and synthesising time waves (particularly sound). This package processes time analysis (oscillograms and envelopes), spectral content, resonance quality factor, cross correlation and autocorrelation, zero-crossing, dominant frequency, 2D and 3D spectrograms.

https://cran.r-project.org/web/packages/seewave/index.html

20.1.2 `sound`

Basic functions for dealing with wav files and sound samples.

https://cran.r-project.org/web/packages/sound/index.html

20.1.3 `tuneR`

Collection of tools to analyse music, handling wave files, transcription.

https://cran.r-project.org/web/packages/tuneR/index.html

20.1.4 `signal`

A set of generally Matlab/Octave-compatible signal processing functions. Includes filter generation utilities, filtering functions, re-sampling routines, and visualisation of filter models. It also includes interpolation functions and some Matlab compatibility functions.

https://cran.r-project.org/web/packages/signal/index.html

A Partial list of packages by category

A.1 Graphics packages

ggplot2 http://ggplot2.org/
lattice https://cran.r-project.org/web/packages/lattice/index.html
rgl https://cran.r-project.org/web/packages/rgl/index.html
tkrplot https://cran.r-project.org/web/packages/tkrplot/index.html
iplots https://cran.r-project.org/web/packages/iplots/index.html
rpanel provides a set of functions to build simple GUI controls for R functions. These are built on the tcltk package. Uses could include changing a parameter on a graph by animating it with a slider or a “doublebutton”, up to more sophisticated control panels. https://cran.r-project.org/web/packages/rpanel/index.html

A.2 GUI packages

Rcmdr https://cran.r-project.org/web/packages/Rcmdr/index.html
JGR https://cran.r-project.org/web/packages/JGR/index.html
pmg Simple GUI for R using gWidgets https://cran.r-project.org/web/packages/pmg/index.html http://www.math.csi.cuny.edu/pmg

A.3 Bibliography management

RefManageR. Provides functions to query PubMed and convert results to BibTeX entries. Query PubMed:
```
hits = ReadPubMed("Nose bleed", database= "PubMed")
```
the retrieved articles can then be turned into BibTeX entries:
```
toBiblatex(hits[1])
```

B Miscellaneous commands

B.1 Data

head(dat) print the first part of the object dat
tail(dat) print the last part of the object dat

B.2 Help

?foo find help on command foo

B.3 Objects

class(foo) get the class of object "foo"
ls() orobjects() list objects present in the workspace

B.4 Organize a session

dir() or list.files()list the files in the current directory
getwd() get the current directory
library(foo) load library foo
library() list all available packages
q() or quit() quit from current session
require(foo) require the library foo, use in scripts
setwd("home/foo") set the working directory
system("foo") execute the system command foo as if it were from the shell

B.5 R administration

library() list all installed packages
R.version info on R version and the platform it is running on

B.6 Syntax

# starts a comment
mydata$foo refer to the variable foo in the dataframe mydata
: interaction operator for model formulae, a:b is the interaction between a and b
* crossing operator for model formulae, a*b = a+b+a:b

C Other manuals and sources of information on R

R Project Homepage http://www.r-project.org/
CRAN http://cran.r-project.org/
R mailing lists http://www.r-project.org/mail.html
Notes on the use of R for psychology experiments and questionnaires by J. Baron and Y. Li http://www.psych.upenn.edu/~baron/rpsych.pdf
Simple R by J.Verzani http://www.math.csi.cuny.edu/Statistics/R/simpleR
Using R for psychological research: A very simple guide to a very elegant package by William Revelle http://personality-project.org/r/
Jonathan Baron’s R page http://finzi.psych.upenn.edu/
Vincent Zoonekynd’s R page http://zoonek2.free.fr/UNIX/48_R/all.html
P.M.E. Altham’s page on multivariate analysis with R notes http://www.statslab.cam.ac.uk/~pat/
Patrick Burns’ R page http://www.burns-stat.com/

C.1 In Italian

Ricerca sociale con R https://www.agnesevardanega.eu/metref/start

C.2 Other useful statistics resources

C.2.1 In Italian

Statistica univariata e bivariata parametrica e non-parametrica per le discipline ambientali e biologiche di Lamberto Soliani http://www.dsa.unipr.it/soliani/soliani.html

D Full colors table

All named colors are listed below:

Figure D.1: Complete color table, part I.

Figure D.2: Complete color table, part II.

Figure D.3: Complete color table, part III.

Figure D.4: Complete color table, part IV.

Figure D.5: Complete color table, part V.

Figure D.6: Complete color table, part VI.

Figure D.7: Complete color table, part VII.

References

Adler, Joseph. 2010. R in a Nutshell. A Desktop Quick Reference. First. Sebastopol, CA: O’Reilly.

Baron, Jonathan, and Yuelin Li. 2003. Notes on the use of R for psychology experiments and questionnaires.

Becker, Richard A, and William S Cleveland. 2002. S-Plus Trellis Graphics User’s Manual. Seattle: MathSoft, Inc., Murray Hill: Bell Labs.

Becker, Richard A, William S Cleveland, and Ming-Jen Shyu. 1996. “The Visual Design and Control of Trellis Display.” Journal of Computational and Graphical Statistics 5: 123–55.

Becker, Richard A, William S Cleveland, Ming-Jen Shyu, and S P Kaluzny. 1996. A Tour of Trellis Graphics.

Cleveland, W. S., and M. Fuentes. 1997. “Trellis Display: Modeling Data from Designed Experiments.” Bell Labs.

Crawley, M. J. 2013. The R Book. Second. Chichester, United Kingdom: Wiley.

Derrick, Ben, Deirdre Toher, and Paul White. 2016. “Why Welch’s Test Is Type I Error Robust.” The Quantitative Methods for Psychology 12 (1): 30–38. https://doi.org/10.20982/tqmp.12.1.p030.

Li, Yuelin, and Jonathan Baron. 2012. Behavioral Research Data Analysis with R. New York, NY: Springer. https://doi.org/10.1007/978-1-4614-1238-0.

Murrell, Paul. 2001. “R Lattice Graphics.” In Proceedings of the 2nd International Workshop on Distributed Statistical Computing, March 15-17, 2001, Technische Universität Wien, Vienna, Austria, edited by Kurt Hornik and Friedrich Leisch. https://www.r-project.org/conferences/DSC-2001/Proceedings/.

Murrell, Paul, and Ross Ihaka. 2000. “An Approach to Providing Mathematical Annotation in Plots.” Journal of Computational and Graphical Statistics 9 (3): 582–99. https://doi.org/10.1080/10618600.2000.10474900.

Sarkar, Deepayan. 2002. “Lattice, an Implementation of Trellis Graphics in R.” R News 2 (2): 19–22.

———. 2003. “Some Notes on Lattice.” In Proceedings of the 3nd International Workshop on Distributed Statistical Computing, March 20-22, 2003, Technische Universität Wien, Vienna, Austria, edited by Kurt Hornik and Friedrich Leisch. https://www.r-project.org/conferences/DSC-2003/Proceedings/.

———. 2008. Lattice: Multivariate Data Visualization with R. New York: Springer. http://lmdvr.r-forge.r-project.org.

Sievert, Carson. 2020. Interactive Web-Based Data Visualization with R, Plotly, and Shiny. Chapman; Hall/CRC. https://plotly-r.com.

Wickham, H. 2009. ggplot2. Elegant Graphics for Data Analysis. New York: Springer-Verlag. https://doi.org/10.1007/978-0-387-98141-3.

———. 2015. R Packages. Sebastopol, CA: O’Reilly. http://r-pkgs.had.co.nz/.

Wilke, Claus O. 2019. Fundamentals of Data Visualization: A Primer on Making Informative and Compelling Figures. Sebastopol, CA: Oreilly & Associates Inc. https://serialmentor.com/dataviz/.

Wilkinson, Leland. 2005. The Grammar of Graphics. Second edition. New York: Springer-Verlag. https://doi.org/10.1007/0-387-28695-0.

Although there are dedicated functions for writing CSV files (write.csv, and write.csv2), they are just wrappers around the write.table function.↩

Number	Scientific Notation	Exponential Notation
\(10\)	\(1\cdot 10^1\)	\(1e1\)
\(20\)	\(2\cdot 10^1\)	\(2e1\)
\(200\)	\(2\cdot 10^2\)	\(2e2\)
\(350\)	\(3.5\cdot 10^2\)	\(3.5e2\)
\(0.00353\)	\(3.53\cdot 10^-3\)	\(3.53e-3\)

	High	Medium	Low	Total
Males	\(6\)	\(11\)	\(27\)	\(44\)
Females	\(25\)	\(30\)	\(12\)	\(67\)
Total	\(31\)	\(41\)	\(39\)	\(111\)

Value	Group	Condition
7	P	1
5	P	1
8	P	1
8	P	1
6	P	1
6	P	2
4	P	2
7	P	2
8	P	2
5	P	2
6	C	1
5	C	1
7	C	1
6	C	1
5	C	1
4	C	2
2	C	2
4	C	2
5	C	2
3	C	2

Value	Drug Exposure	Word Type	Participant
7	D	C	1
5	D	C	2
8	D	C	3
8	D	C	4
6	D	C	5
6	D	A	1
4	D	A	2
7	D	A	3
8	D	A	4
5	D	A	5
6	N	C	1
5	N	C	2
7	N	C	3
6	N	C	4
5	N	C	5
4	N	A	1
2	N	A	2
4	N	A	3
5	N	A	4
3	N	A	5

Value	Group	Condition
7	P	1
5	P	1
8	P	1
8	P	1
6	P	1
6	P	2
4	P	2
7	P	2
8	P	2
5	P	2
6	C	1
5	C	1
7	C	1
6	C	1
5	C	1
4	C	2
2	C	2
4	C	2
5	C	2
3	C	2

Value	Drug Exposure	Word Type	Participant
7	D	C	1
5	D	C	2
8	D	C	3
8	D	C	4
6	D	C	5
6	D	A	1
4	D	A	2
7	D	A	3
8	D	A	4
5	D	A	5
6	N	C	1
5	N	C	2
7	N	C	3
6	N	C	4
5	N	C	5
4	N	A	1
2	N	A	2
4	N	A	3
5	N	A	4
3	N	A	5

A R Guide

0.4.0